Structural Design of Foundations for the Home Inspector

by Nick Gromicko, CMI® and Ben Gromicko

General

• crawlspace;
• basement;
• slab-on-grade with stem wall;
• monolithic slab;
• piles;
• piers; and
• alternative methods.

The most common residential foundation materials are concrete masonry (i.e., concrete block) and cast-in-place concrete. Preservative-treated wood, precast concrete, and other methods may also be used. The concrete slab on grade is the most popular foundation type in the Southeast; basements are the most common type in the East and Midwest. Crawlspaces are common in the Northwest and Southeast. Pile foundations are commonly used in coastal flood zones to elevate structures above flood levels, in weak or expansive soils to reach a stable stratum, and on steeply sloped sites.

 Figure 4.1 Types of Foundations

 

 

A crawlspace is a building foundation that uses a perimeter foundation wall to create an under-floor space that is not habitable; the interior crawlspace elevation may or may not be below the exterior finish grade. A basement is typically defined as a portion of a building that is partly or completely below the exterior grade and that may be used as habitable or storage space. 

A slab on grade with an independent stem wall is a concrete floor supported by the soil independently of the rest of the building. The stem wall supports the building loads and, in turn, is supported directly by the soil or a footing. A monolithic or thickened-edge slab is a ground-supported slab on grade with an integral footing (i.e., thickened edge); it is normally used in warmer regions with little or no frost depth but is also used in colder climates when adequate frost protection is provided.

When necessary, piles are used to transmit the load to a deeper soil stratum with a higher bearing capacity to prevent failure due to undercutting of the foundation by scour from floodwater flow at high velocities, and to elevate the building above required flood elevations. Piles are also used to isolate the structure from expansive soil movements.

Post-and-pier foundations can provide an economical alternative to crawlspace perimeter wall construction. It is common practice to use a brick curtain wall between piers for appearance and bracing purposes.

The design procedures and information in this section covers:

• foundation materials and properties;
• soil-bearing capacity and footing size;
• concrete or gravel footings;
• concrete and masonry foundation walls;
• preservative-treated wood walls;
• insulating concrete foundations;
• concrete slabs on grade;
• pile foundations; and
• frost protection.

Concrete design procedures generally follow the strength design method contained in ACI (American Concrete Institute)-318 (ACI, 1999), although certain aspects of the procedures may be considered conservative relative to conventional residential foundation applications. For this reason, some supplemental design guidance is provided when practical and technically justified. Masonry design procedures follow the allowable stress design method of ACI-530 (ACI, 1999). Wood design procedures are used to design the connections between the foundation system and the structure above and follow the allowable stress design method for wood construction. In addition, the designer is referred to the applicable design standards for symbol definitions and additional guidance, since the intent of this article is to provide supplemental instruction in the efficient design of residential foundations.

Material Properties

A residential designer using concrete and masonry materials must have a basic understanding of such materials, as well as an appreciation of variations in the materials’ composition and structural properties. In addition, soils are considered a foundation material. A brief discussion of the properties of concrete and masonry follows.

Concrete

Concrete is a mixture of cement, water, sand, gravel, crushed rock, or other aggregates. Sometimes, one or more admixtures are added to change certain characteristics of the concrete, such as workability, durability, and time of hardening. The proportions of the components determine the concrete mix’s compressive strength and durability.

Type

Portland cement is classified into several types in accordance with ASTM C150 (ASTM, 1998). Residential foundation walls are typically constructed with Type I cement, which is a general-purpose Portland cement used for the vast majority of construction projects. Other types of cement are appropriate in accommodating conditions related to heat of hydration in massive pours and sulfate resistance. In some regions, sulfates in soils have caused durability problems with concrete. The designer should check into local conditions and practices.

Weight

The weight of concrete varies depending on the type of aggregates used in the concrete mix. Concrete is typically referred to as lightweight or normal-weight. The density of unreinforced normal weight concrete ranges between 144 and 156 pounds per cubic foot (pcf) and is typically assumed to be 150 pcf. Residential foundations are constructed with normal-weight concrete.

Slump

Slump is the measure of concrete consistency; the higher the slump, the wetter the concrete and the easier it flows. Slump is measured in accordance with ASTM C143 (ASTM, 1998) by inverting a standard 12-inch-high metal cone, filling it with concrete, and then removing the cone; the amount the concrete settles in units of inches is the slump. Most foundations, slabs, and walls consolidated by hand methods have a slump between 4 and 6 inches. One problem associated with a high-slump concrete is segregation of the aggregate, which leads to cracking and scaling. Therefore, a slump of greater than 6 should be avoided.

Admixtures

Admixtures are materials added to the concrete mix to improve workability and durability and to retard or accelerate curing. Some of the most common admixtures include:

• water reducers to improve the workability of concrete without reducing its strength;
• retarders used in hot weather to allow more time for placing and finishing concrete. Retarders may also reduce the early strength of concrete;
• accelerators to reduce the setting time, allowing less time for placing and finishing concrete. Accelerators may also increase the early strength of concrete; and
• air-entrainers used for concrete that will be exposed to freeze-thaw conditions and de-icing salts. Less water is needed, and desegregation of aggregate is reduced when air-entrainers are added.
  
  

Reinforcement

Concrete has high compressive strength but low tensile strength; therefore, reinforcing steel is often embedded in the concrete to provide additional tensile strength and ductility. In the rare event that the capacity may be exceeded, the reinforcing steel begins to yield, eliminating an abrupt failure that may otherwise occur in plain, unreinforced concrete. For this reason, a larger safety margin is used in the design of plain concrete construction than in reinforced concrete construction.

Steel reinforcement is available in Grade 40 or Grade 60; the grade number refers to the minimum tensile yield strength of the steel (Grade 40 is minimum 40 ksi steel and Grade 60 is minimum 60 ksi steel). Either grade may be used for residential construction; however, most reinforcement in the U.S. market today is Grade 60. It is also important that the concrete mix or slump be adjusted through the addition of an appropriate amount of water to allow the concrete to flow easily around the reinforcement bars, particularly when the bars are closely spaced or crowed at points of overlap. However, close spacing is rarely required in residential construction and should be avoided in design.

The most common steel reinforcement or rebar sizes in residential construction are No. 3, No. 4, and No. 5, which correspond to diameters of 3/8-inch, 1/2-inch, and 5/8-inch, respectively. These three sizes of rebar are easily handled at the jobsite by using manual bending and cutting devices. Table 4.1 provides useful relationships among the rebar number, diameter, and cross-sectional areas for reinforced concrete and masonry design.

 

Concrete Masonry Units

In residential construction, nominal 8-inch-thick concrete masonry units are readily available. It is generally more economical if the masonry unit's compressive strength ranges between 1,500 and 3,000 psi. The standard block used in residential and light-frame commercial construction is generally rated with a design strength of 1,900 psi, although other strengths are available.

Grade

Concrete masonry units are described by grades according to their intended use per ASTM C90 (ASTM, 1999) or C129 (ASTM, 1999). Residential foundation walls should be constructed with Grade N units. Grade S may be used above grade. The grades are described below.

• Grade N is typically required for general use, such as in interior and backup walls, and in above- or below-grade exterior walls that may or may not be exposed to moisture penetration or the weather.
• Grade S is typically limited to above-grade use in exterior walls with weather-protective coatings, and in walls not exposed to the weather.

Type

Concrete masonry units are classified in accordance with ASTM C90 as Type I or II (ASTM, 1999). Type I is a moisture-controlled unit that is typically specified where drying shrinkage of the block due to moisture loss may result in excessive cracking in the walls. Type II is a non-moisture-controlled unit that is suitable for all other uses. Residential foundation walls are typically constructed with Type II units.

Weight

Concrete masonry units are available with different densities by altering the type(s) of aggregate used in their manufacture. Concrete masonry units are typically referred to as lightweight, medium-weight, or normal-weight, with respective unit weights or densities less than 105 pcf, between 105 and 125 pcf, and more than 125 pcf.

Residential foundation walls are typically constructed with low- to medium-weight units because of the low compressive strength required. However, lower-density units are generally more porous and must be properly protected to resist moisture intrusion. A common practice in residential basement foundation wall construction is to provide a cement-based parge coating and a brush- or spray-applied bituminous coating on the below-ground portions of the wall. This treatment is usually required by code for basement walls of masonry or concrete construction; however, in concrete construction, the parge coating is not necessary.

Hollow or Solid

Concrete masonry units are classified as hollow or solid in accordance with ASTM C90 (ASTM, 1999). The net concrete cross-sectional area of most concrete masonry units ranges from 50 to 70%, depending on unit width, face-shell and web thicknesses, and core configuration. Hollow units are defined as those in which the net concrete cross-sectional area is less than 75% of the gross cross-sectional area. Solid units are not necessarily solid but are defined as those in which the net concrete cross-sectional area is 75% of the gross cross-sectional area or greater.

Mortar

Masonry mortar is used to join concrete masonry units into a structural wall; it also retards air and moisture infiltration. The most common way to lay block is in a running bond pattern where the vertical head joints between blocks are offset by half the block's length from one course to the next. Mortar is composed of cement, lime, clean, well-graded sand, and water, and is typically classified into Types M, S, N, O, and K in accordance with ASTM C270 (ASTM, 1999). Residential foundation walls are typically constructed with Type M or Type S mortar, both of which are generally recommended for load-bearing interior and exterior walls, including above- and below-grade applications.

Grout

Grout is a slurry consisting of cementitious material, aggregate and water. When needed, grout is commonly placed in the hollow cores of concrete masonry units to provide a wall with added strength. In reinforced load-bearing masonry wall construction, grout is usually placed only in those hollow cores containing steel reinforcement. The grout bonds the masonry units and steel so that they act as a composite unit to resist imposed loads. Grout may also be used in unreinforced concrete masonry walls for added strength.

Soil-Bearing Capacity and Footing Size

 

 

When a soil-bearing investigation is desired to determine more accurate and economical footing requirements, the designer commonly turns to ASTM D1586, Standard Penetration Test (SPT) and Split-Barrel Sampling of Soils (ASTM, 1999). This test relies on a 2-inch-diameter device driven into the ground with a 140-pound hammer dropped from a distance of 30 inches. The number of hammer drops or blows needed to create a 1-foot penetration (or blow count) is recorded. Values can be roughly correlated to soil-bearing values as shown in Table 4.3. The instrumentation and cost of conducting the SPT test is usually not warranted for typical residential applications. Nonetheless, the SPT test method provides information on deeper soil strata and thus can offer valuable guidance for foundation design and building location, particularly when subsurface conditions are suspected to be problematic. The values in Table 4.3 are associated with the blow count from the SPT test method. Many engineers can provide reasonable estimates of soil-bearing by using smaller penetrometers at less cost, although such devices and methods may require an independent calibration to determine presumptive soil-bearing values and may not be able to detect deep subsurface problems. Calibrations may be provided by the manufacturer or, alternatively, developed by the engineer.

The designer should exercise judgment when selecting the final design value, and be prepared to make adjustments (increases or decreases) in interpreting and applying the results to a specific design. The values in Tables 4.2 and 4.3 are generally associated with a safety factor of 3 (Naval Facilities Engineering Command, 1996) and are considered appropriate for non-continuous or independent spread footings supporting columns or piers (point loads). Use of a minimum safety factor of 2 (corresponding to a higher presumptive soil-bearing value) is recommended for smaller structures with continuous spread footings, such as houses. To achieve a safety factor of 2, the designer may multiply the values in Tables 4.2 and 4.3 by 1.5.

Table 4.3 Presumptive Soil-Bearing Values (psf) Based on Standard Penetrometer Blow Count 

 

Notes:

• 1 N denotes the standard penetrometer blow count in blows per foot, in accordance with ASTM D1586; shown in parentheses.
• 2 Compaction should be considered in these conditions, particularly when the blow count is five blows per foot or less.
• 3 Pile and grade beam foundations should be considered in these conditions, particularly when the blow count is five blows per foot or less.

The required width or area of a spread footing is determined by dividing the building load on the footing by the soil-bearing capacity from Table 4.2 or Table 4.3, as shown below. Building design loads, including dead and live loads, should be determined by using allowable stress design (ASD) load combinations.

Footings

The objectives of footing design are:

• to provide a level surface for construction of the foundation wall;
• to provide adequate transfer and distribution of building loads to the underlying soil;
• to provide adequate strength, in addition to the foundation wall, to prevent differential settlement of the building in weak or uncertain soil conditions;
• to place the building foundation at a sufficient depth to avoid frost heave or thaw weakening in frost-susceptible soils and to avoid organic surface soil layers; and
• to provide adequate anchorage or mass (when needed in addition to the foundation wall) to resist potential uplift and overturning forces resulting from high winds or severe seismic events.

In the next section, we'll learn about design methods for concrete and gravel footings.

By far, the most common footing in residential construction is a continuous concrete spread footing. However, concrete and gravel footings are both recognized in prescriptive footing size tables in residential building codes for most typical conditions (ICC, 1998). In contrast, special conditions give rise to some engineering concerns that need to be addressed to ensure the adequacy of any foundation design. 

Special conditions include:

• steeply sloped sites requiring a stepped footing;
• high-wind conditions;
• inland or coastal flooding conditions;
• high-hazard seismic conditions; and
• poor soil conditions.

Building codes for residential construction contain tables that prescribe minimum footing widths for plain concrete footings (ICC, 1998). Alternatively, footing widths may be determined in accordance with Section 4.3 based on a site’s particular loading condition and presumptive soil-bearing capacity. The following are general rules of thumb for determining the thickness of plain concrete footings for residential structures, once the required bearing width is calculated:

• The minimum footing thickness should not be less than the distance the footing extends outward from the edge of the foundation wall, or 6 inches, whichever is greater.
• The footing width should project a minimum of 2 inches from both faces of the wall (to allow for a minimum construction tolerance), but not greater than the footing thickness.

These rules of thumb generally result in a footing design that differs somewhat from the plain concrete design provisions of Chapter 22 of ACI-318. It should also be understood that footing widths generally follow the width increments of standard excavation equipment (a backhoe bucket size of 12, 16 or 24 inches). Even though some designers and builders may specify one or two longitudinal No. 4 bars for wall footings, steel reinforcement is not required for residential-scale structures in typical soil conditions. For situations where the rules of thumb or prescriptive code tables do not apply or where a more economical solution is possible, a more detailed footing analysis may be considered.

Much like a concrete footing, a gravel footing may be used to distribute foundation loads to a sufficient soil-bearing surface area. It also provides a continuous path for water or moisture and thus must be drained in accordance with the foundation drainage provisions of the national building codes. Gravel footings are constructed of crushed stone or gravel that is consolidated by tamping or vibrating. Pea gravel, which is naturally consolidated, does not require compaction and can be screeded to a smooth, level surface much like concrete. Although typically associated with pressure-treated wood foundations, a gravel footing can support cast-in-place or precast concrete foundation walls.

The size of a gravel footing is usually based on a 30- to 45-degree angle of repose for distributing loads; therefore, as with plain concrete footings, the required depth and width of the gravel footing depends on the width of the foundation wall, the foundation load, and soil-bearing values. Following a rule of thumb similar to that for a concrete footing, the gravel footing thickness should be no less than 1.5 times its extension beyond the edge of the foundation wall, or, in the case of a pressure-treated wood foundation, the mud sill. Just as with a concrete footing, the thickness of a gravel footing may be considered in meeting the required frost depth. In soils that are not naturally well-drained, provision should be made to adequately drain a gravel footing.

Concrete Footing Design

For the vast majority of residential footing designs, it quickly becomes evident that conventional residential footing requirements found in residential building codes are adequate, if not conservative (ICC,1998). However, to improve performance and economy or to address peculiar conditions, a footing may need to be specially designed.

A footing is designed to resist the upward-acting pressure created by the soil beneath the footing; that pressure tends to make the footing bend upward at its edges. According to ACI-318, the three modes of failure considered in reinforced concrete footing design are one-way shear, two-way shear, and flexure. Bearing (crushing) is also a possible failure mode, but is rarely applicable to residential loading conditions. To simplify calculations for the three failure modes, the following discussion explains the relation of the failure modes to the design of plain and reinforced concrete footings. The designer should refer to ACI-318 for additional commentary and guidance. The design equations used later in this section are based on ACI-318 and principles of engineering mechanics as described below. Moreover, the approach is based on the assumption of uniform soil-bearing pressure on the bottom of the footing; therefore, walls and columns should be supported as close as possible to the center of the footings.

One-Way (Beam) Shear

When a footing fails due to one-way (beam) shear, the failure occurs at an angle approximately 45 degrees to the wall, as shown in Figure 4.2. For plain concrete footings, the soil-bearing pressure has a negligible effect on the diagonal shear tension for distance t from the wall edge toward the footing edge; for reinforced concrete footings, the distance used is d, which equals the depth to the footing rebar (see Figure 4.2). As a result, one-way shear is checked by assuming that beam action occurs at a critical failure plane extending across the footing width, as shown in Figure 4.2. One-way shear must be considered in similar fashion in both continuous wall and rectangular footings; however, for ease of calculation, continuous wall footing design is typically based on one lineal foot of wall/footing.

Two-Way (Punching) Shear

When a footing fails by two-way (punching) shear, the failure occurs at an angle approximately 30 degrees to the column or pier, as shown in Figure 4.2. Punching shear is rarely a concern in the design of continuous wall footings and thus is usually checked only in the case of rectangular or circular footings with a heavily loaded pier or column that creates a large concentrated load on a relatively small area of the footing. For plain concrete footings, the soil-bearing pressure has a negligible effect on the diagonal shear tension at distance t/2 from the face of a column toward the footing edges; for reinforced concrete footings, the distance from the face of the column is d/2 (see Figure 4.2). Therefore, the shear force consists of the net upward-acting pressure on the area of the footing outside the “punched-out” area (hatched area in Figure 4.2). For square, circular or rectangular footings, shear is checked at the critical section that extends in a plane around a concrete, masonry, wood, or steel column or pier that forms the perimeter of the area described above.

FIGURE 4.2 Critical Failure Planes in Continuous or Square Concrete

 Flexure (Bending)

The maximum moment in a footing deformed by the upward-acting soil pressures would logically occur in the middle of the footing; however, the rigidity of the wall or column above resists some of the upward-acting forces and affects the location of maximum moment. As a result, the critical flexure plane for footings supporting a rigid wall or column is assumed to be located at the face of the wall or column. Flexure in a concrete footing is checked by computing the moment created by the soil-bearing forces acting over the cantilevered area of the footing that extends from the critical flexure plane to the edge of the footing (hatched area in Figure 4.2). The approach for masonry walls in ACI-318 differs slightly in that the failure plane is assumed to be located one-fourth of the way under a masonry wall or column, creating a slightly longer cantilever. For the purpose of this guide, the difference is considered unnecessary.

Bearing Strength

It is difficult to contemplate conditions where concrete bearing or compressive strength is a concern in typical residential construction; therefore, a design check can usually be dismissed as “OK by inspection.” In rare and peculiar instances where bearing compressive forces on the concrete are extreme and approach or exceed the specified concrete compressive strength, ACI-318•10.17 and ACI-318•12.3 should be consulted for appropriate design guidance.

Plain Concrete Footing Design

In this section, the design of plain concrete footings is presented by using the concepts related to shear and bending covered in the previous section.

Shear

 

 

Reinforced Concrete Footing Design

For infrequent situations in residential construction where a plain concrete footing may not be practical, or where it is more economical to reduce the footing thickness, steel reinforcement may be considered. A reinforced concrete footing is designed similar to a plain concrete footing; however, the concrete depth d to the reinforcing bar is used to check shear instead of the entire footing thickness t. The depth of the rebar is equal to the thickness of the footing minus the diameter of the rebar db and the concrete cover c. In addition, the moment capacity is determined differently due to the presence of the reinforcement, which resists the tension stresses induced by the bending moment. Finally, a higher resistance factor is used to reflect the more consistent bending strength of reinforced concrete relative to unreinforced concrete.

As specified by ACI-318, a minimum of 3 inches of concrete cover over steel reinforcement is required when concrete is in contact with soil. In addition, ACI-318 does not permit a depth d less than 6 inches for reinforced footings supported by soil. These limits may be relaxed by the designer, provided that adequate capacity is demonstrated in the strength analysis; however, a reinforced footing thickness of significantly less than 6 inches may be considered impractical even though it may calculate acceptably. One exception may be found where a nominal 4-inch-thick slab is reinforced to serve as an integral footing for an interior load-bearing wall (that is not intended to transmit uplift forces from a shear wall overturning restraint anchorage in high-hazard wind or seismic regions). Further, the concrete cover should not be less than 2 inches for residential applications, although this recommendation may be somewhat conservative for interior footings that are generally less exposed to ground moisture and other corrosive agents.

Shear

In the equations given below for one- and two-way shear, the dimensions are in accordance with Figure 4.2; units of inches should be used. Shear reinforcement (stirrups) is usually considered impractical for residential footing construction; therefore, the concrete is designed to withstand the shear stress as expressed in the equations. The equations are specifically tailored for footings supporting walls or square columns, since such footings are common in residential construction. The equations may be generalized for use with other conditions (e.g., rectangular footings and rectangular columns, round footings, etc.) by following the same principles. In addition, the terms 3√f’c and 4√f’c are in units of pounds per square inch and represent “lower-bound” estimates of the ultimate shear stress capacity of reinforced concrete.

Flexure

The flexure equations below pertain specifically to reinforced concrete footings that support walls or square columns. The equations may be generalized for use with other conditions (e.g., rectangular footings and rectangular columns, round footings, etc.) by following the same principles. The alternative equation for nominal moment strength Mn is derived from force and moment equilibrium principles by using the provisions of ACI-318. Most designers are familiar with the alternative equation that uses the reinforcement ratio ρand the nominal strength coefficient of resistance Rn. The coefficient is derived from the design check that ensures that the factored moment (due to factored loads) Mu is less than the factored nominal moment strength φMn of the reinforced concrete. To aid the designer in shortcutting these calculations, design manuals provide design tables that correlate the nominal strength coefficient of resistance Rn to the reinforcement ratio ρfor a specific concrete compressive strength and steel yield strength.

 

 

Designers often specify one or two longitudinal No. 4 bars for wall footings as nominal reinforcement in the case of questionable soils, or when required to maintain continuity of stepped footings on sloped sites, or under conditions resulting in a changed footing depth. However, for most residential foundations, the primary resistance against differential settlement is provided by the deep beam action of the foundation wall; footing reinforcement may provide limited benefit. In such cases, the footing simply acts as a platform for the wall construction and distributes loads to a larger soil-bearing area.

Lap Splices

Where reinforcement cannot be installed in one length to meet reinforcement requirements (as in continuous wall footings), reinforcement bars must be lapped to develop the bars’ full tensile capacity across the splice. In accordance with ACI-318, a minimum lap length of 40 times the diameter of the reinforcement bar is required for splices in the reinforcement. In addition, the separation between spliced or lapped bars is not to exceed eight times the diameter of the reinforcement bar, or 6 inches, whichever is less.

Foundation Walls

The objectives of foundation wall design are:

• to transfer the load of the building to the footing or directly to the earth;
• to provide adequate strength, in combination with the footing (when required) to prevent differential settlement;
• to provide adequate resistance to shear and bending stresses resulting from lateral soil pressure;
• to provide anchorage for the above-grade structure to resist wind or seismic forces;
• to provide a moisture-resistant barrier to below-ground habitable space in accordance with the building code; and
• to isolate non-moisture-resistant building materials from the ground.

In some cases, masonry or concrete foundation walls incorporate a nominal amount of steel reinforcement to control cracking. Engineering specifications generally require reinforcement of concrete or masonry foundation walls because of somewhat arbitrary limits on minimum steel-to-concrete ratios, even for “plain” concrete walls. However, residential foundation walls are generally constructed of unreinforced or nominally reinforced concrete or masonry or of preservative-treated wood. The nominal reinforcement approach has provided many serviceable structures. This section discusses the issue of reinforcement and presents rational design approach for residential concrete and masonry foundation walls.

In most cases, a design for concrete or concrete masonry walls can be selected from the prescriptive tables in the applicable residential building code or the International One- and Two-Family Dwelling Code (ICC, 1998). Sometimes, a specific design applied with reasonable engineering judgment results in a more efficient and economical solution than that prescribed by the codes. The designer may elect to design the wall as either a reinforced or a plain concrete wall. The following sections detail design methods for both wall types.

Concrete Foundation Walls

Regardless of the type of concrete foundation wall selected, the designer needs to determine the nominal and factored loads that, in turn, govern the type of wall (reinforced or unreinforced) that may be appropriate for a given application. The following LRFD load combinations are suggested for the design of residential concrete foundation walls:

• 1.2 D + 1.6 H
• 1.2 D + 1.6 H + 1.6 L + 0.5 (Lr or S)
• 1.2 D + 1.6 H + 1.6 (Lr or S) + 0.5 L

In light-frame homes, the first load combination typically governs foundation wall design. Axial load increases moment capacity of concrete walls when they are not appreciably eccentric, as is the case in typical residential construction.

To simplify the calculations further, the designer may conservatively assume that the foundation wall acts as a simple span beam with pinned ends, although such an assumption will tend to over-predict the stresses in the wall. In any event, the simple span model requires the wall to be adequately supported at its top by the connection to the floor framing, and at its base by the connection to the footing or bearing against a basement floor slab. Appendix A contains basic load diagrams and beam equations to assist the designer in analyzing typical loading conditions and element-based structural actions encountered in residential design. Once the loads are known, the designer can perform design checks for various stresses by following ACI-318 and the recommendations contained herein.

As a practical consideration, residential designers need to keep in mind that concrete foundation walls are typically 6, 8 or 10 inches thick (nominal). The typical concrete compressive strength used in residential construction is 2,500 or 3,000 psi, although other strengths are available. Typical reinforcement tensile yield strength is 60,000 psi (Grade 60) and is primarily a matter of market supply.

Plain Concrete Wall Design

ACI-318 allows the design of plain concrete walls with some limits, as discussed in ACI-318•220.  ACI-318 recommends the incorporation of contraction and isolation joints to control cracking; however, this is not a typical practice for residential foundation walls, and temperature and shrinkage cracking is practically unavoidable. It is considered to have a negligible impact on the structural integrity of a residential wall. However, cracking may be controlled (minimize potential crack widening) by reasonable use of horizontal reinforcement.

ACI-318 limits plain concrete wall thickness to a minimum of 7-1/2 inches; however, the International One- Two-Family Dwelling Code (ICC, 1998) permits nominal 6-inch-thick foundation walls when the height of unbalanced fill is less than a prescribed maximum. The 7-1/2-inch-minimum thickness requirement is obviously impractical for a short concrete stem wall, as in a crawlspace foundation.

Adequate strength needs to be provided and should be demonstrated by analysis in accordance with the ACI-318 design equations and the recommendations in this section. Depending on soil loads, analysis should confirm conventional residential foundation wall practice in typical conditions.

The following checks are used to determine if a plain concrete wall has adequate strength.

Shear Capacity

If greater shear capacity is required in a plain concrete wall, it may be obtained by increasing the wall thickness or increasing the concrete's compressive strength. Alternatively, a wall can be reinforced.

The following equations apply to both perpendicular and parallel shear in conjunction with Figure 4.3 for plain concrete walls. For parallel shear, the equations do not address overturning and bending action that occurs in a direction parallel to the wall, particularly for short segments of walls under significant parallel shear load. For concrete foundation walls, this is generally not a concern.

 

 

 

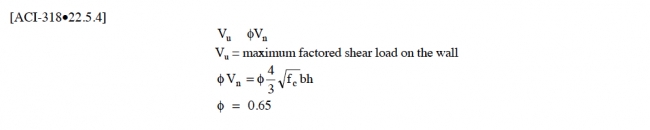
 Combined Axial and Bending Capacity

The ACI-318 equations listed below account for the combined effects of axial load and bending moment on a plain concrete wall. The intent is to ensure that the concrete face in compression and the concrete face in tension resulting from factored nominal axial and bending loads do not exceed the factored nominal capacity for concrete.

 

Even though a plain concrete wall often calculates as adequate, the designer may elect to add a nominal amount of reinforcement for crack control or other reasons. Walls determined inadequate to withstand combined axial load and bending moment may gain greater capacity through increased wall thickness or increased concrete compressive strength. Alternatively, the wall may be reinforced. Walls determined to have adequate strength to withstand shear and combined axial load and bending moment may also be checked for deflection, but this is usually not a limiting factor for typical residential foundation walls.

Reinforced Concrete Design

ACI-318 allows two approaches to the design of reinforced concrete with some limits on wall thickness and the minimum amount of steel reinforcement; however, ACI-318 also permits these requirements to be waived in the event that structural analysis demonstrates adequate strength and stability in accordance with ACI-318•14.2.7.

Reinforced concrete walls should be designed in accordance with ACI318•14.4 by using the strength design method. The following checks for shear and combined flexure and axial load determine if a wall is adequate to resist the applied loads.

Shear Capacity

Shear stress is a result of the lateral loads on a structure associated with wind, earthquake, or lateral soil forces. The loads are, however, either normal to the wall surface (perpendicular or out of plane) or parallel to the wall surface (in plane). The designer must check both perpendicular and parallel shear in the wall to determine if the wall can resist the lateral loads present.

If greater shear capacity is required, it may be obtained by increasing the wall thickness, increasing the concrete compressive strength, adding horizontal shear reinforcement, or installing vertical reinforcement to resist shear through shear friction. Shear friction is the transfer of shear through friction between two faces of a crack. Shear friction also relies on resistance from protruding portions of concrete on either side of the crack and by dowel action of the reinforcement that crosses the crack. The maximum limit on reinforcement spacing of 12 or 24 inches specified in ACI-318•11.5.4 is considered to be an arbitrary limit. When reinforcement is required, 48 inches as an adequate maximum spacing for residential foundation wall design agrees with practical experience.

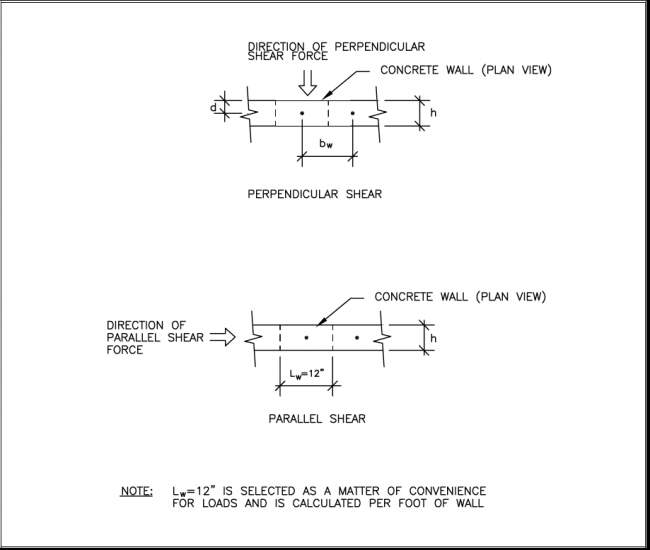
The following equations provide checks for both perpendicular and parallel shear in conjunction with Figure 4.4. For parallel shear, the equations do not address overturning and bending action that occurs in a direction parallel to the wall, particularly for short segments of walls under significant parallel shear load. For concrete foundation walls, this is generally not a concern.



FIGURE 4.4 Variables Defined for Shear Calculations in Reinforced Concrete Walls

Combined Flexural and Axial Load Capacity

ACI-318 prescribes reinforcement requirements for concrete walls. Foundation walls commonly resist both an applied axial load from the structure above and an applied lateral soil load from backfill. To ensure that the wall’s strength is sufficient, the designer must first determine slenderness effects (Euler buckling) in the wall. ACI-318•10.10 provides an approximation method to account for slenderness effects in the wall; however, the slenderness ratio must not be greater than 100. The slenderness ratio is defined in the following section as the ratio between unsupported length and the radius of gyration. In residential construction, the approximation method, more commonly known as the moment magnifier method, is usually adequate because slenderness ratios are typically less than 100 in foundation walls.

The moment magnifier method is based on the wall’s classification as a “sway frame” or “non-sway frame.” In concept, a sway frame is a frame (columns and beams) as opposed to a concrete bearing wall system. Sway frames are not discussed in detail herein because the soil pressures surrounding a residential foundation typically provide lateral support to resist any racking and deflections associated with a sway frame. More important, foundation walls generally have few openings and thus do not constitute a frame-like system. For more information on sway frames and their design procedure, refer to ACI318•10.13.

The moment magnifier method uses the relationship of the axial load and lateral load in addition to wall thickness and unbraced height to determine a multiplier of 1 or greater, which accounts for slenderness in the wall. The multiplier is termed the moment magnifier. It magnifies the calculated moment in the wall resulting from the lateral soil load and any eccentricity in axial load. Together, the axial load and magnified moment are used to determine whether the foundation wall section is adequate to resist the applied loads. 

The following steps are required to determine the amount of reinforcement required in a typical residential concrete foundation wall to resist combined flexure and axial loads:

• calculate axial and lateral loads;
• verify that the non-sway condition applies;
• calculate slenderness;
• calculate the moment magnifier; and
• plot the axial load and magnified moment on an interaction diagram.

The following sections discuss the procedure in detail.

Slenderness

Conservatively, assuming that the wall is pinned at the top and bottom, slenderness in the wall can be calculated by using the equation below. The effective length factor k is conservatively assumed to equal 1 in this condition. It should be noted that a value of k much less than 1 (i.e., 0.7) may actually better represent the end conditions (non-pinned) of residential foundation walls.

 

Moment Magnifier Method

The moment magnifier method is an approximation method allowed in ACI318•10.10 for concrete walls with a slenderness ratio less than or equal to 100. If the slenderness ratio is less than 34, then the moment magnifier is equal to 1 and requires no additional analysis. The design procedure and equations below follow ACI-318•10.12. The equation for EI, as listed in ACI-318, is applicable to walls containing a double layer of steel reinforcement. Residential walls typically contain only one layer of steel reinforcement; therefore, the equation for EI, as listed herein, is based on Section 10.12 (ACI, 1996).

 

TABLE 4.4 Simplified Moment Magnification Factors

Interaction Diagrams

An interaction diagram is a graphic representation of the relationship between the axial load and bending capacity of a reinforced or plain concrete wall. The primary use of interaction diagrams is as a design aid for selecting predetermined concrete wall or column designs for varying loading conditions. Several publications provide interaction diagrams for use with concrete. These publications, however, typically focus on column or wall design that is heavily reinforced in accordance with design loads common in commercial construction. Residential concrete walls are either plain or slightly reinforced, with one layer of reinforcement typically placed near the center of the wall. Plain and reinforced concrete interaction diagrams for residential applications and the methods for deriving them may be found in Structural Design of Insulating Concrete Form Walls in Residential Construction (PCA, 1998). PCA also offers a computer program that plots interaction diagrams based on user input; the program is entitled PCA Column (PCACOL).

An interaction diagram assists the designer in determining the wall’s structural adequacy at various loading conditions (combinations of axial and bending loads). Figure 4.5 illustrates interaction diagrams for plain and reinforced concrete. Both the design points located within the interaction curve for a given wall height and the reference axes represent a combination of axial load and bending moment that the wall can safely support. The most efficient design is close to the interaction diagram curve. For residential applications, the designer, realizing that the overall design process is not exact, usually accepts designs within plus or minus 5% of the interaction curve.

FIGURE 4.5 Typical Interaction Diagrams for Plain and Reinforced Concrete Walls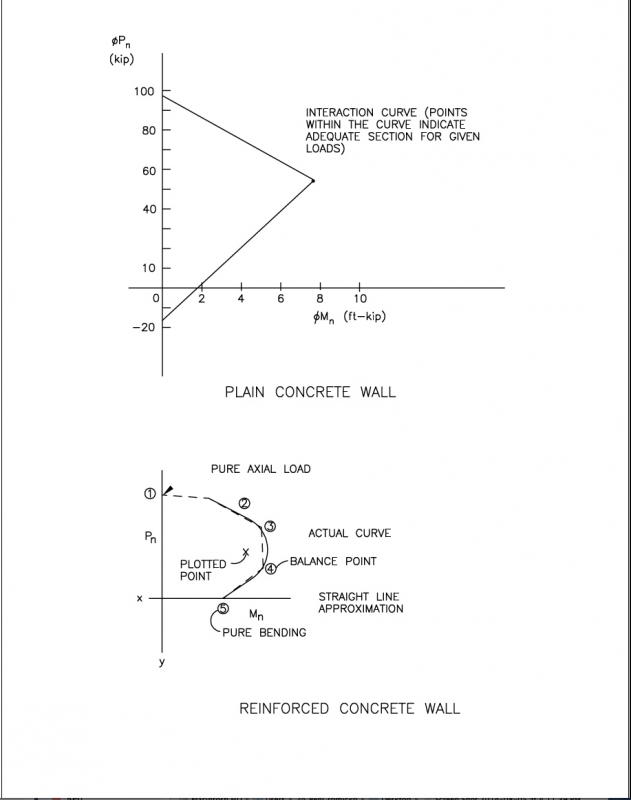


 Minimum Concrete Wall Reinforcement

Concrete Wall Deflection

ACI-318 does not specifically limit wall deflection. Therefore, deflection is usually not analyzed in residential foundation wall design. Regardless, a deflection limit of L/240 for unfactored soil loads is not unreasonable for below-grade walls.

When using the moment magnifier method, the designer is advised to apply the calculated moment magnification factor to the unfactored load moments used in conducting the deflection calculations. The calculation of wall deflection should also use effective section properties based on EcIg for plain concrete walls and EcIe for reinforced concrete walls; refer to ACI 318•9.5.2.3 to calculate the effective moment of inertia, Ie.

If unfactored load deflections prove unacceptable, the designer may increase the wall thickness or the amount of vertical wall reinforcement. For most residential loading conditions, however, satisfying reasonable deflection requirements should not be a limiting condition.

Concrete Wall Lintels

Openings in concrete walls are constructed with concrete, steel, precast concrete, cast stone, or reinforced masonry wall lintels. Wood headers are also used when not supporting concrete construction above and when continuity at the top of the wall (i.e., bond beam) is not critical, as in high-hazard seismic or hurricane coastal zones, or is maintained sufficiently by a wood sill plate and other construction above.

This section focuses on the design of concrete lintels. The concrete lintel is often assumed to act as a simple span with each end pinned. However, the assumption implies no top reinforcement to transfer the moment developed at the end of the lintel. Under that condition, the lintel is assumed to be cracked at the ends such that the end moment is zero and the shear must be transferred from the lintel to the wall through the bottom reinforcement.

If the lintel is assumed to act as a fixed-end beam, sufficient embedment of the top and bottom reinforcement beyond each side of the opening should be provided to fully develop a moment-resisting end in the lintel. Though more complicated to design and construct, a fixed-end beam reduces the maximum bending moment on the lintel and allows increased spans. A concrete lintel cast in a concrete wall acts somewhere between a true simple span beam and a fixed-end beam. Thus, a designer may design the bottom bar for a simple span condition and the top bar reinforcement for a fixed-end condition (conservative). Often, a No. 4 bar is placed at the top of each wall story to help tie the walls together (bond beam) which can also serve as the top reinforcement for concrete lintels. Figure 4.6 depicts the cross-section and dimensions for analysis of concrete lintels.

For additional information on concrete lintels and their design procedure, refer to the Structural Design of Insulating Concrete Form Walls in Residential Construction (PCA, 1998) and to Testing and Design of Lintels Using Insulating Concrete Forms (HUD, 2000). The latter demonstrates through testing that shear reinforcement (stirrups) of concrete lintels is not necessary for short spans (3 feet or less) with lintel depths of 8 inches or more. This research also indicates that the minimum reinforcement requirements in ACI-318 for beam design are conservative when a minimum #4 rebar is used as bottom reinforcement. Further, lintels with small span-to-depth ratios can be accurately designed as deep beams in accordance with ACI-318 when the minimum reinforcement ratios are met; refer to ACI-318•11.4.

FIGURE 4.6 Design Variables Defined for Lintel Bending and Shear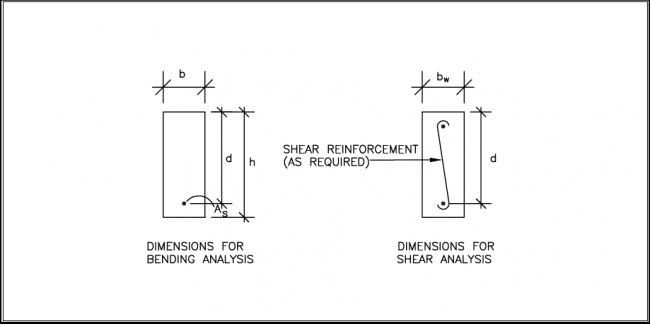


 Flexural Capacity

The following equations are used to determine the flexural capacity of a reinforced concrete lintel in conjunction with Figure 4.6. An increase in the lintel depth or area of reinforcement is suggested if greater bending capacity is required. As a practical matter, though, lintel thickness is limited to the thickness of the wall in which a lintel is placed. In addition, lintel depth is often limited by the floor-to-floor height and the vertical placement of the opening in the wall. Therefore, in many cases, increasing the amount or size of reinforcement is the most practical and economical solution.

 Shear Capacity

Concrete lintels are designed for shear resulting from wall, roof, and floor loads in accordance with the equations below and Figure 4.6.

 

 Check Concrete Lintel Deflection

Masonry Foundation Walls

Masonry foundation wall construction is common in residential construction. It is used in a variety of foundation types, including basements, crawlspaces, and slabs on grade. For prescriptive design of masonry foundation walls in typical residential applications, a designer or builder may use the International One- and Two-Family Dwelling Code (ICC, 1998) or the local residential building code.

ACI-530 provides for the design of masonry foundation walls by using allowable stress design (ASD). Therefore, design loads may be determined according to load combinations as follows:

• D + H
• D + H + L + 0.3 (Lr or S)
• D + H + (Lr or S) + 0.3 L

In light-frame homes, the first load combination typically governs masonry walls. To simplify the calculations, the designer may conservatively assume that the wall story acts as a simple span with pinned ends, although such an assumption may tend to over-predict the stresses in the wall. Walls that are determined to have adequate strength to withstand shear and combined axial load and bending moment generally satisfy unspecified deflection requirements. Therefore, foundation wall deflection is not discussed in this section. However, if desired, deflection may be considered for concrete foundation walls.

To follow the design procedure, the designer needs to know the strength properties of various types and grades of masonry, mortar, and grout currently available on the market. With the loads and material properties known, the designer can then perform design checks for various stresses by following ACI-530. Residential construction rarely involves detailed masonry specifications but rather makes use of standard materials and methods familiar to local suppliers and trades.

An engineer’s inspection of a home is hardly ever required under typical residential construction conditions. Designers should be aware, however, that in jurisdictions covered by the Uniform Building Code (ICBO, 1997), lack of inspection on the jobsite requires reductions in the allowable stresses to account for potentially greater variability in material properties and workmanship. Indeed, a higher level of inspection should be considered when masonry construction is specified in high-hazard seismic or severe hurricane areas. ACI-530 makes no distinction between inspected and non-inspected masonry walls and, therefore, does not require adjustments in allowable stresses based on level of inspection.

As a residential designer, keep in mind that concrete masonry units (block) are readily available in nominal 6-, 8-, 10- and 12-inch thicknesses. It is generally more economical if the masonry unit's compressive strength ranges between 1,500 and 3,000 psi. The standard block used in residential and light commercial construction is usually rated at 1,900 psi.

Unreinforced Masonry Design

ACI-530 addresses the design of unreinforced masonry to ensure that unit stresses and flexural stresses in the wall do not exceed certain maximum allowable stresses. It provides for two methods of design: an empirical design approach and an allowable stress design approach.

Walls may be designed in accordance with ACI-530•5 by using the empirical design method under the following conditions:

• The building is not located in Seismic Design Category D or E as defined in NEHRP-97 or ASCE 7-98 (i.e., Seismic Zones 3 or 4 in most current and local building codes).
• Foundation walls do not exceed 8 feet in unsupported height.
• The length of the foundation walls between perpendicular masonry walls or pilasters is a maximum of 3 times the basement wall height. This limit typically does not apply to residential basements as required in the International One- and Two-Family Dwelling Code (ICC, 1998) and other similar residential building codes.
• Compressive stresses do not exceed the allowable stresses listed in ACI-530; compressive stresses are determined by dividing the design load by the gross cross-sectional area of the unit per ACI-530•5.4.2.
• Backfill heights do not exceed those listed in Table 4.5.
• Backfill material is non-expansive and is tamped no more than necessary to prevent excessive settlement.
• Masonry is laid in running bond with Type M or S mortar.
• Lateral support is provided at the top of the foundation wall before backfilling.

Drainage is important when using the empirical table because lack of good drainage may substantially increase the lateral load on the foundation wall if the soil becomes saturated. As required in standard practice, the finish grade around the structure should be adequately sloped to drain surface water away from the foundation walls. The backfill material should also be drained to remove ground water from poorly drained soils.

Wood floor framing typically provides lateral support to the top of masonry foundation walls and therefore should be adequately connected to the masonry in accordance with one of several options. The most common method of connection calls for a wood sill plate, anchor bolts, and nailing of the floor framing to the sill plate.

When the limits of the empirical design method are exceeded, the allowable stress design procedure for unreinforced masonry, as detailed below, provides a more flexible approach by which walls are designed as compression and bending members in accordance with ACI-530•2.2.

TABLE 4.5 Nominal Wall Thickness for 8-Foot-High Foundation Walls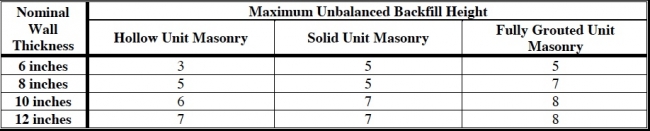


Walls may be designed in accordance with ACI-530•2.2 by using the allowable stress design method. The fundamental assumptions, derivation of formulas, and design procedures are similar to those developed for strength-based design for concrete except that the material properties of masonry are substituted for those of concrete. Allowable masonry stresses used in allowable stress design are expressed in terms of a fraction of the specified compressive strength of the masonry at the age of 28 days. A typical fraction of the specified compressive strength is 0.25 or 0.33, which equates to a conservative safety factor between 3 and 4 relative to the minimum specified masonry compressive strength. Design values for flexural tension stress are given in Table 4.6. The following design checks are used to determine if an unreinforced masonry wall is structurally adequate

TABLE 4.6 Allowable Flexural Tension Stresses for Allowable Stress Design of Unreinforced Masonry 


 Shear Capacity

Shear stress is a result of the lateral loads on the structure associated with wind, earthquakes or backfill forces. Lateral loads are both normal to the wall surface (perpendicular or out of plane) and parallel to the wall surface (parallel or in plane). Both perpendicular and parallel shear should be checked; however, neither perpendicular nor parallel shear is usually a controlling factor in residential foundation walls.

If greater perpendicular shear capacity is required, it may be obtained by increasing the wall thickness, increasing the masonry unit compressive strength, or adding vertical reinforcement in grouted cells. If greater parallel shear capacity is required, it may be obtained by increasing the wall thickness, reducing the size or number of wall openings, or adding horizontal joint reinforcement. Horizontal truss-type joint reinforcement can substantially increase parallel shear capacity, provided that it is installed properly in the horizontal mortar bed joints. If not installed properly, it can create a place of weakness in the wall, particularly in out-of-plane bending of an unreinforced masonry wall.

The equations below are used to check perpendicular and parallel shear in masonry walls. The variable Nv is the axial design load acting on the wall at the point of maximum shear. The equations are based on An, which is the net cross-sectional area of the masonry. For parallel shear, the equations do not address overturning and bending action that occurs in a direction parallel to the wall, particularly for short segments of walls under significant parallel shear load. For concrete foundation walls, this is generally not a concern.

 

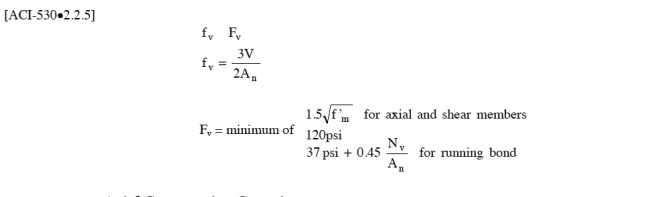
 Axial Compression Capacity

The following equations from ACI-530•2.3 are used to design masonry walls and columns for compressive loads only. They are based on the net cross-sectional area of the masonry, including grouted and mortared areas.



 Combined Axial Compression and Flexural Capacity

The following equations from ACI-530 determine the relationship of the combined effects of axial load and bending moment on a masonry wall.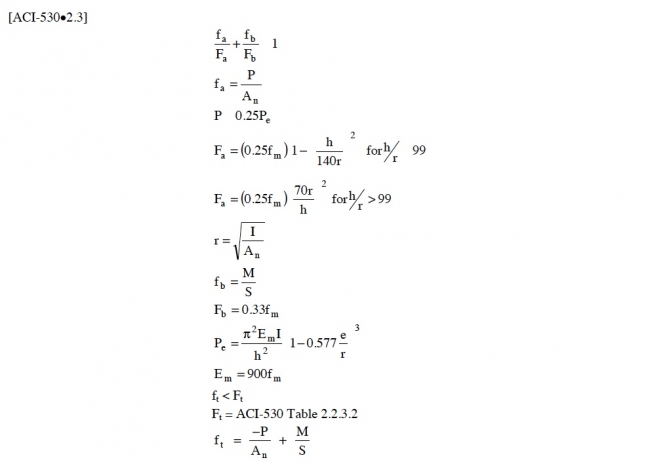


Tension Capacity

ACI-530 provides allowable values for flexural tension transverse to the plane of a masonry wall. Standard principles of engineering mechanics determine the tension stress due to the bending moment caused by lateral (soil) loads and offset by axial loads (dead loads).


Even though an unreinforced masonry wall may calculate as adequate, the designer may consider adding a nominal amount of reinforcement to control cracking.

Walls determined inadequate to withstand combined axial load and bending moment may gain greater capacity through increased wall thickness, increased masonry compressive strength, or the addition of steel reinforcement.

Usually, the most effective and economical solution for providing greater wall capacity in residential construction is to increase wall thickness, although reinforcement is also common.

Reinforced Masonry Design

When unreinforced concrete masonry wall construction does not satisfy all design criteria (e.g., load, wall thickness limits, etc.), reinforced walls may be designed by following the allowable stress design procedure or the strength-based design procedure of ACI-530. The allowable stress design procedure outlined below describes an approach by which walls are designed in accordance with ACI-530•2.3. Although not discussed in detail herein, walls may also be designed by following the strength-based design method specified in ACI-530.

For walls designed in accordance with ACI-530•2.3 using the allowable stress design method, the fundamental assumptions, derivation of formulas, and design procedures are similar to those for design for concrete except that the material properties of masonry are substituted for those of concrete. Allowable masonry stresses used in allowable stress design are expressed in terms of a fraction of the specified compressive strength of the masonry at the age of 28 days. A typical fraction of the specified compressive strength is 0.25, which equates to a conservative safety factor of 4. The following design checks determine if a reinforced masonry wall is structurally adequate.

Shear Capacity

Shear stress is a result of lateral loads on the structure associated with wind, earthquakes or backfill forces. Lateral loads are both normal to the wall surface (perpendicular or out of plane) and parallel to the wall surface (parallel or in plane). Both perpendicular and parallel shear should be checked, however, perpendicular shear is rarely a controlling factor in the design of masonry walls and parallel shear is not usually a controlling factor unless the foundation is partially or fully above grade (i.e., walk-out basement) with a large number of openings.

The equations below check perpendicular and parallel shear in conjunction with Figure 4.7. Some building codes include a “j” coefficient in these equations. The “j” coefficient defines the distance between the center of the compression area and the center of the tensile steel area; however, it is often dismissed or approximated as 0.9. If greater parallel shear capacity is required, it may be obtained in a manner similar to that recommended in the previous section for unreinforced masonry design. For parallel shear, the equations do not address overturning and bending action that occurs in a direction parallel to the wall, particularly for short segments of walls under significant parallel shear load. For concrete foundation walls, this is generally not a concern.



If the shear stress exceeds the above allowables for masonry only, the designer must design shear reinforcing with the shear stress equation changes in accordance with ACI-530•2.3.5. In residential construction, it is generally more economical to increase the wall thickness or to grout additional cores instead of using shear reinforcement. If shear reinforcement is desired, refer to ACI-530. ACI-530 limits vertical reinforcement to a maximum spacing s of 48 inches; however, a maximum of 96 inches on-center is suggested as adequate. Masonry homes built with reinforcement at 96 inches on-center have performed well in hurricane-prone areas, such as southern Florida.

Flexural or axial stresses must be accounted for to ensure that a wall is structurally sound. Axial loads increase compressive stresses and reduce tension stresses and may be great enough to keep the masonry in an uncracked state under a simultaneous bending load.

Axial Compression Capacity

The following equations from ACI-530•2.3 are used to determine if a masonry wall can withstand conditions when compressive loads act only on walls and columns (e.g., interior load-bearing wall or floor beam support pier). As with concrete, compressive capacity is usually not an issue in supporting a typical light-frame home. An exception may occur with the bearing points of long-spanning beams. In such a case, the designer should check bearing capacity by using ACI-530•2.1.7.

FIGURE 4.7 Variables Defined for Shear Calculations in Reinforced Concrete Masonry Walls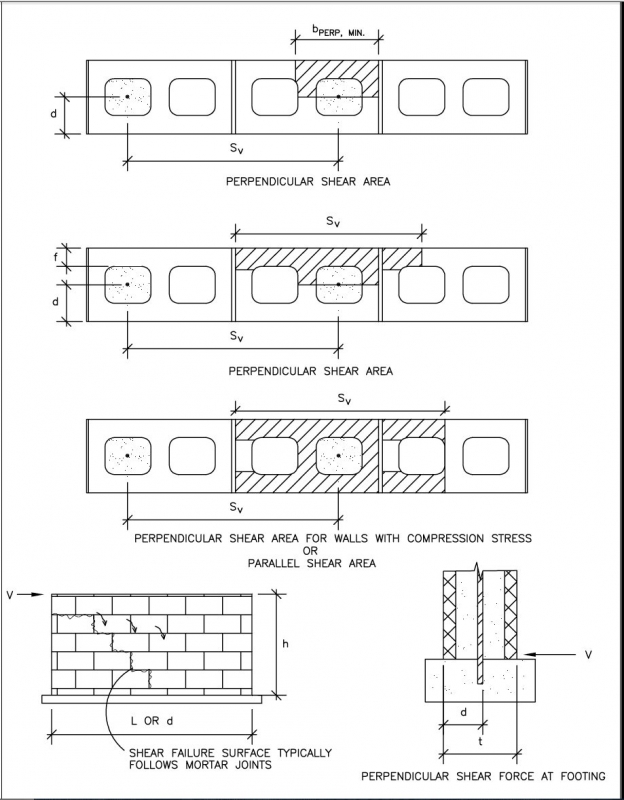

Calculation using the above equations is based on Ae, which is the effective cross-sectional area of the masonry, including grouted and mortared areas substituted for An.

Combined Axial Compression and Flexural Capacity

In accordance with ACI-530•2.3.2, the design tensile forces in the reinforcement due to flexure shall not exceed 20,000 psi for Grade 40 or 50 steel, 24,000 psi for Grade 60 steel, or 30,000 psi for wire joint reinforcement. As stated, most reinforcing steel in the U.S. market today is Grade 60. The following equations pertain to walls that are subject to combined axial and flexure stresses.



Walls determined inadequate to withstand combined axial load and bending moment may gain greater capacity through increased wall thickness, increased masonry compressive strength, or added steel reinforcement.

Minimum Masonry Wall Reinforcement

Unreinforced concrete masonry walls have proven serviceable in millions of homes. Builders and designers may, however, wish to specify a nominal amount of reinforcement even when such reinforcement is not required by analysis. For example, it is not uncommon to specify horizontal reinforcement to control shrinkage cracking and to improve the bond between intersecting walls. When used, horizontal reinforcement is typically specified as a ladder or truss-type wire reinforcement. It is commonly installed continuously in mortar joints at vertical intervals of 24 inches (every third course of block).

For reinforced concrete masonry walls, ACI-530 stipulates minimum reinforcement limits as shown below; however, the limits are somewhat arbitrary and have no tangible basis as a minimum standard of care for residential design and construction. The designer should exercise reasonable judgment based on application conditions, experience in local practice, and local building code provisions for prescriptive masonry foundation or above-grade wall design in residential applications.



 Masonry Wall Lintels

Openings in masonry walls are constructed by using steel, precast concrete, or reinforced masonry lintels. Wood headers are also used when they do not support masonry construction above and when continuity at the top of the wall (bond beam) is not required or is adequately provided within the system of wood-framed construction above. Steel angles are the simplest shapes and are suitable for openings of moderate width typically found in residential foundation walls. The angle should have a horizontal leg of the same width as the thickness of the concrete masonry that it supports. Openings may require vertical reinforcing bars with a hooked end that is placed on each side of the opening to restrain the lintel against uplift forces in high-hazard wind or earthquake regions. Building codes typically require steel lintels exposed to the exterior to be a minimum 1/4-inch thick. Figure 4.8 illustrates some lintels commonly used in residential masonry construction.

FIGURE 4.8 Concrete Masonry Wall Lintel Types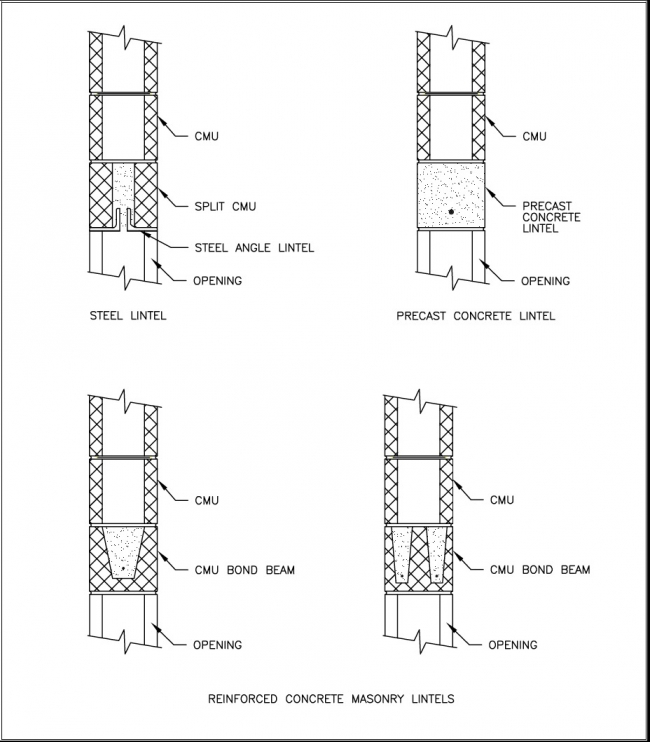


Many prescriptive design tables are available for lintel design.

Preservative-Treated Wood Foundation Walls

Preservative-treated wood foundations, commonly known as permanent wood foundations (PWF), have been used in over 300,000 homes and other structures throughout the United States. When properly installed, they provide foundation walls at an affordable cost. In some cases, the manufacturer may offer a 50-year material warranty, which exceeds the warranty offered for other common foundation materials.

A PWF is a load-bearing, preservative-treated, wood-framed foundation wall sheathed with preservative-treated plywood; it bears on a gravel spread footing. PWF lumber and plywood used in foundations is pressure treated with calcium chromium arsenate (CCA) to a minimum retention of 0.6 pcf. The walls are supported laterally at the top by the floor system and at the bottom by a cast-in-place concrete slab or pressure-treated lumber floor system or by backfill on the inside of the wall. Proper connection details are essential, along with provisions for drainage and moisture protection. All fasteners and hardware used in a PWF should be stainless steel or hot-dipped galvanized. Figure 4.9 illustrates a PWF.

PWFs may be designed in accordance with the basic provisions provided in the International One- and Two-Family Dwelling Code (ICC, 1998). Those provisions, in turn, are based on the Southern Forest Products Association’s Permanent Wood Foundations Design and Construction Guide (SPC, 1998). The PWF guide offers design flexibility and thorough technical guidance. Table 4.7 summarizes some basic rules of thumb for design. The steps for using the prescriptive tables are outlined below.

FIGURE 4.9 Preservative-Treated Wood Foundation Walls


 TABLE 4.7 Preservative-Treated Wood Foundation Framing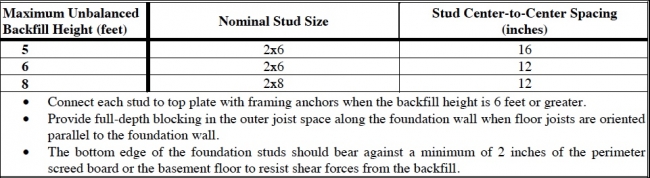

• Granular (gravel or crushed rock) footings are sized accordingly. Permanent wood foundations may also be placed on poured concrete footings.
• Footing plate size is determined by the vertical load from the structure on the foundation wall and the size of the permanent wood foundation studs.
• The size and spacing of the wall framing is selected from tables for buildings up to 36 feet wide that support one or two stories above grade.
• APA-rated plywood is selected from tables based on unbalanced backfill height and stud spacing. The plywood must be preservative-treated and rated for below-ground application.
• Drainage systems are selected in accordance with foundation type (e.g., basement or crawlspace) and soil type. Foundation wall moisture-proofing is also required (i.e., polyethylene sheeting).

For more information on preservative-treated wood foundations and their specific design and construction, consult the Permanent Wood Foundations Design and Construction Guide (SPC, 1998).

Insulating Concrete Form Foundation Walls

Insulating concrete forms (ICFs) have been used in the United States since the 1970s. They provide durable and thermally efficient foundation and above-grade walls at reasonable cost. Insulating concrete forms are constructed of rigid foam plastic, composites of cement and plastic foam insulation or wood chips, or other suitable insulating materials that have the ability to act as forms for cast-in-place concrete walls. The forms are easily placed by hand and remain in place after the concrete is cured to provide added insulation.

ICF systems are typically categorized with respect to the form of the ICF unit. There are three types of ICF forms: hollow blocks, planks and panels. The shape of the concrete wall is best visualized with the form stripped away, exposing the concrete to view. 

ICF categories based on the resulting nature of the concrete wall are listed below.

• flat:  solid concrete wall of uniform thickness;
• post-and-beam:  concrete frame constructed of vertical and horizontal concrete members with voids between the members created by the form. The spacing of the vertical members may be as great as 8 feet;
• screen-grid:  concrete wall composed of closely spaced vertical and horizontal concrete members with voids between the members created by the form. The wall resembles a thick screen made of concrete; and
• waffle-grid:  concrete wall composed of closely space vertical and horizontal concrete members with thin concrete webs filling the space between the members. The wall resembles a large waffle made of concrete.

Foundations may be designed in accordance with the values provided in the most recent national building codes’ prescriptive tables (ICC, 1998). Manufacturers also usually provide design and construction information. Special consideration must be given to the dimensions and shape of an ICF wall that is not a flat concrete wall. Refer to Figure 4.10 for a typical ICF foundation wall detail.

FIGURE 4.10 Insulating Concrete Form Foundation Walls


For more design information, refer to the Structural Design of Insulating Concrete Form Walls in Residential Construction (Lemay and Vrankar, 1998). For a prescriptive construction approach, consult the Prescriptive Method for Insulating Concrete Forms in Residential Construction (HUD, 1998).

Slabs on Grade

The primary objectives of slab-on-grade design are:

• to provide a floor surface with adequate capacity to support all applied loads;
• to provide thickened footings for attachment of the above grade structure and for transfer of the load to the earth where required; 
• and to provide a moisture barrier between the earth and the interior of the building.

Many concrete slabs for homes, driveways, garages, and sidewalks are built according to standard thickness recommendations and do not require a specific design unless poor soil conditions, such as expansive clay soils, exist on the site.

For typical loading and soil conditions, floor slabs, driveways, garage floors, and residential sidewalks are built at a nominal 4 inches thick per ACI302•2.1. Where interior columns and load-bearing walls bear on the slab, the slab is typically thickened and may be nominally reinforced. Monolithic slabs may also have thickened edges that provide a footing for structural loads from exterior load-bearing walls. The thickened edges may or may not be reinforced in standard residential practice.

Slab-on-grade foundations are often placed on 2 to 3 inches of washed gravel or sand and a 6 mil (0.006 inch) polyethylene vapor barrier. This recommended practice prevents moisture in the soil from wicking through the slab. The sand or gravel layer acts primarily as a capillary break to soil moisture transport through the soil. If tied into the foundation drain system, the gravel layer can also help provide drainage.

A slab on grade greater than 10 feet in any dimension will likely experience cracking due to temperature and shrinkage effects that create internal tensile stresses in the concrete. To prevent the cracks from becoming noticeable, the designer usually specifies some reinforcement, such as welded wire fabric (WWF) or a fiber-reinforced concrete mix. The location of cracking may be controlled by placing construction joints in the slab at regular intervals or at strategic locations hidden under partitions or under certain floor finishes (e.g., carpet).

In poor soils where reinforcement is required to increase the slab’s flexural capacity, the designer should follow conventional reinforced concrete design methods. The Portland Cement Association (PCA), Wire Reinforcement Institute (WRI), and U.S. Army Corps of Engineers (COE) espouse three methods for the design of plain or reinforced concrete slabs on grade.

Presented in chart or tabular format, the PCA method selects a slab thickness in accordance with the applied loads and is based on the concept of one equivalent wheel loading at the center of the slab. Structural reinforcement is typically not required; however, a nominal amount of reinforcement is suggested for crack control, shrinkage, and temperature effects.

The WRI method selects a slab thickness in accordance with a discrete-element computer model for the slab. The WRI approach graphically accounts for the relative stiffness between grade support and the concrete slab to determine moments in the slab. The information is presented in the form of design nomographs.

Presented in charts and tabular format, the COE method is based on Westergaard’s formulae for edge stresses in a concrete slab and assumes that the unloaded portions of the slab help support the slab portions under direct loading.

For further information on the design procedures for each design method mentioned above and for unique loading conditions, refer to ACI-360, Design of Slabs on Grade (ACI, 1998) or the Design and Construction of Post-Tensioned Slabs on Ground (PTI, 1996) for expansive soil conditions.

Pile Foundations

Piles support buildings under a variety of special conditions that make conventional foundation practices impractical or inadvisable. 

Such conditions include:

• weak soils or non-engineered fills that require the use of piles to transfer foundation loads by skin friction or point bearing;
• inland floodplains and coastal flood hazard zones where buildings must be elevated;
• steep or unstable slopes; and
• expansive soils where buildings must be isolated from soil expansion in the “active” surface layer and anchored to stable soil below.

Piles are available in a variety of materials. Preservative-treated timber piles are typically driven into place by a crane with a mechanical or drop hammer (most common in weak soils and coastal construction). Concrete piles or piers are typically cast in place in drilled holes, sometimes with “belled” bases (most common in expansive soils). Steel H-piles or large-diameter pipes are typically driven or vibrated into place with specialized heavy equipment (uncommon in residential construction).

Timber piles are most commonly used in light-frame residential construction. The minimum pile capacity is based on the required foundation loading. Pile capacity is, however, difficult to predict; therefore, only rough estimates of required pile lengths and sizes can be made before installation, particularly when the designer relies only on skin friction to develop capacity in deep, soft soils. For this reason, local successful practice is a primary factor in any pile foundation design such that a pile foundation often can be specified by experience with little design effort. In other cases, some amount of subsurface exploration (i.e., standard pertrometer test) is advisable to assist in foundation design or, alternatively, to indicate when one or more test piles may be required.

It is rare for pile depth to be greater than 8 or 10 feet except in extremely soft soils, on steeply sloped sites with unstable soils, or in coastal hazard areas (beachfront property) where significant scour is possible due to storm surge velocity. Under these conditions, depths can easily exceed 10 feet. In coastal high-hazard areas known as “V zones” on flood insurance rating maps (FIRMs), the building must be elevated above the 100-year flood elevation, which is known as the base flood elevation (BFE) and includes an allowance for wave height. As shown in Figure 4.11, treated timber piles are typically used to elevate a structure.

FIGURE 4.11 Basic Coastal Foundation Construction


For additional guidance, the designer is referred to the Coastal Construction Manual (FEMA, 1986) and Pile Buck (Pile Buck, 1990) but should be prepared to make reasonable design modifications and judgments based on personal experience with and knowledge of pile construction and local conditions. National flood Insurance Program (NFIP) requirements should also be carefully considered by the designer since they may affect the availability of insurance and the premium amount. From a life-safety perspective, pile-supported buildings are often evacuated during a major hurricane, but flood damage can be substantial if the building is not properly elevated and detailed. In these conditions, the designer must consider several factors, including flood loads, wind loads, scour, breakaway wall and slab construction, corrosion, and other factors. The publications of the Federal Emergency Management Agency (FEMA), Washington, D.C., offer design guidance. FEMA is also in the process of updating the Coastal Construction Manual.

The habitable portion of buildings in coastal “A zones” (non-velocity flow) and inland floodplains must be elevated above the BFE, particularly if flood insurance is to be obtained. However, piles are not necessarily the most economical solution. Common solutions include fills to build up the site or the use of crawlspace foundations.

 

In the above equation, Pa is the net allowable vertical load capacity, Wr is the hammer ram weight, h is the distance the hammer free falls, s is the pile penetration (set) per blow at the end of driving, and F is the safety factor. The units for s and h must be the same. The value of s may be taken as the inverse of the blow count for the last foot of driving. Using the above equation, a “test” pile may be evaluated to determine the required pile length to obtain adequate bearing.

Alternatively, the designer can specify a required minimum penetration and required number of blows per foot to obtain sufficient bearing capacity by friction. The pile size may be specified as a minimum tip diameter, a minimum butt diameter, or both. The minimum pile butt diameter should not be less than 8 inches; 10- to 12-inch diameters are common. The larger pile diameters may be necessary for unbraced conditions with long unsupported heights.

In hard material or densely compacted sand or hard clay, a typical pile meets “refusal” when the blows per foot become excessive. In such a case, it may be necessary to jet or pre-drill the pile to a specific depth to meet the minimum embedment and then finish with several hammer blows to ensure that the required capacity is met and the pile properly seated in firm soil.

Jetting is the process of using a water pump, hose, and long pipe to “jet” the tip of the pile into hard-driving ground, such as firm sand. Jetting may also be used to adjust the pile vertically to maintain a reasonable tolerance with the building layout dimension.

It is also important to connect or anchor the building properly to pile foundations when severe uplift or lateral load conditions are expected. For standard pile and concrete grade beam construction, the pile is usually extended into the concrete “cap” a few inches or more. The connection requirements of the National Design Specification for Wood Construction (NDS, 1997) should be carefully followed for these heavy-duty connections.

Frost Protection

The objective of frost protection in foundation design is to prevent damage to the structure from frost action (heaving and thaw weakening) in frost-susceptible soils.

Conventional Methods

In northern U.S. climates, builders and designers mitigate the effects of frost heave by constructing homes with perimeter footings that extend below a locally prescribed frost depth. 

Other construction methods include:

• piles or caissons extending below the seasonal frost line;
• mat or reinforced structural slab foundations that resist differential heave;
• non-frost-susceptible fills and drainage; and
• adjustable foundation supports.

The local building department typically sets required frost depths. Often, the depths are highly conservative in accordance with frost depths experienced in applications not relevant to residential foundations. The local design frost depth can vary significantly from that required by actual climate, soil, and application conditions. One exception occurs in Alaska, where it is common to specify different frost depths for “warm,” “cold,” and “interior” foundations. For homes in the Anchorage, Alaska, area, the perimeter foundation is generally classified as warm, with a required depth of 4 or 5 feet. Interior footings may be required to be 8 inches deep. On the other hand, “cold” foundations, including outside columns, may be required to be as much as 10 feet deep. In the contiguous 48 states, depths for footings range from a minimum 12 inches in the South to as much as 6 feet in some northern localities.

Based on the air-freezing index, Table 4.8 presents minimum “safe” frost depths for residential foundations. Figure 4.12 depicts the air-freezing index, a climate index closely associated with ground freezing depth. The most frost-susceptible soils are silty soils or mixtures that contain a large fraction of silt-sized particles. Generally, soils or fill materials with less than 6% fines (as measured by a #200 sieve) are considered non-frost-susceptible. Proper surface water and foundation drainage are also important factors where frost heave is a concern. The designer should recognize that many soils may not be frost-susceptible in their natural state (e.g., sand, gravel, or other well-drained soils that are typically low in moisture content). However, for those that are frost-susceptible, the consequences can be significant and costly if not properly considered in the foundation design.

TABLE 4.8 Minimum Frost Depths for Residential Footings


 Frost-Protected Shallow Foundations

A frost-protected shallow foundation (FPSF) is a practical alternative to deeper foundations in cold regions characterized by seasonal ground freezing and the potential for frost heave. Figure 4.13 illustrates several FPSF applications. FPSFs are best suited to slab-on-grade homes on relatively flat sites. The FPSF method may, however, be used effectively with walkout basements by insulating the foundation on the downhill side of the house, thus eliminating the need for a stepped footing.

An FPSF is constructed by using strategically placed vertical and horizontal insulation to insulate the footings around the building, thereby allowing foundation depths as shallow as 12 inches in very cold climates. The frost-protected shallow foundation technology recognizes earth as a heat source that repels frost. Heat input to the ground from buildings therefore contributes to the thermal environment around the foundation.

The thickness of the insulation and the horizontal distance that the insulation must extend away from the building depends primarily on the climate. In less severe cold climates, horizontal insulation is not necessary. Other factors, such as soil thermal conductivity, soil moisture content, and the internal temperature of a building are also important. Current design and construction guidelines are based on reasonable worst-case conditions.

After more than 40 years of use in the Scandinavian countries, FPSFs are now recognized in the prescriptive requirements of the International One- and Two- Family Dwelling Code. However, the code places limits on the use of foam plastic below grade in areas of noticeably high termite infestation probability. In those areas termite barriers or other details must be incorporated into the design to block hidden pathways leading from the soil into the structure between the foam insulation and the foundation wall. The exception to the code limit occurs when termite-resistant materials (e.g., concrete, steel, or preservative-treated wood) are specified for a home’s structural members.

FIGURE 4.12 Air-Freezing Index Map (100-Year Return Period)


The complete design procedure for FPSFs is detailed in Frost-Protected Shallow Foundations in Residential Construction. The first edition of this guide is available from the U.S. Department of Housing and Urban Development. Either version provides useful construction details and guidelines for determining the amount (thickness) of insulation required for a given climate or application. Acceptable insulation materials include expanded and extruded polystyrenes, although adjusted insulation values are provided for below-ground use. The American Society of Civil Engineers (ASCE) is currently developing a standard for FPSF design and construction based on the resources mentioned above.

 

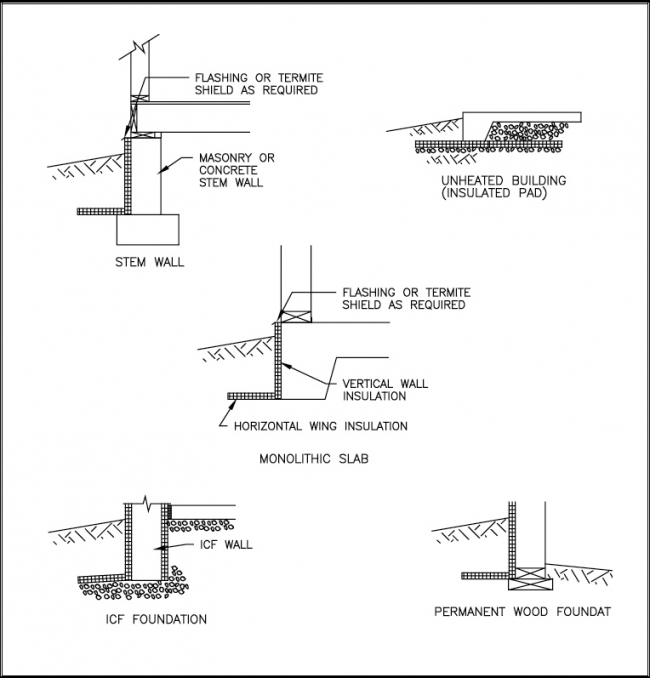
 Permafrost