Structural Design of Wood Framing for the Home Inspector
by Nick Gromicko, CMI® and Ben Gromicko

General
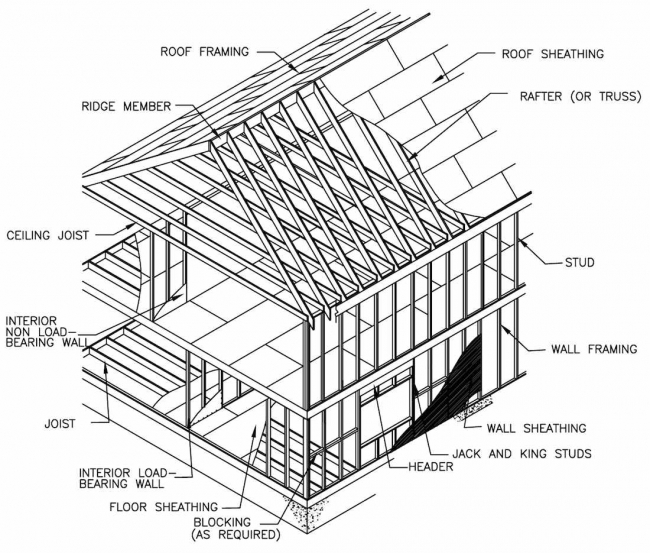
This article addresses elements of above-grade structural systems in residential construction. The residential construction material most commonly used above grade in North America is light-frame wood; therefore, we'll focus on structural design that specifies standard-dimension lumber and structural wood panels (i.e., plywood and oriented strand-board sheathing). Design of the lateral force-resisting system (shear walls and diaphragms) must be approached from a system design perspective. Connections and their importance relative to the overall performance of wood-framed construction cannot be overemphasized. The basic components and assemblies of a conventional wood frame home are shown in Figure 5.1.Many elements of a home work together as a system to resist lateral and axial forces imposed on the above-grade structure and transfer them to the foundation. The above-grade structure also helps resist lateral soil loads on foundation walls through the connection of the floor system to the foundation. Therefore, the issue of system performance is most pronounced in the above-grade assemblies of light-frame homes. Within the context of simple engineering approaches that are familiar to inspectors, system-based design principles are addressed here.
The design of the above-grade structure involves the following structural systems and assemblies:

Wood members that are in contact with the ground should be preservative-treated. The most common lumber treatment is CCA (copper chromium arsenate), which should be used for applications such as sill plates located near the ground and for exterior decks. It is important to specify the correct level of treatment: 0.4 pcf retention for non-ground-contact exterior exposure, and 0.6 pcf for ground contact.
Termites and other wood-destroying insects (e.g., carpenter ants, boring beetles, etc.) attack wood materials. Some practical solutions include: the chemical treatment of soil; the installation of physical barriers (e.g., termite shields); and the specification of treated lumber.
Termites are a special problem in warmer climates, although they also plague many other areas of the United States. The most common termites are subterranean termites that nest in the ground and enter wood that is near or in contact with damp soil. They gain access to above-grade wood through cracks in the foundation or through shelter tubes (mud tunnels) on the surface of foundation walls. Since the presence of termites lends itself to visual detection, wood-framed homes require periodic inspection for signs of termites.
Structural Wood Panels
Historically, boards were used for roof, floor, and wall sheathing; in the last 30 years, however, structural wood panel products have come to dominate the sheathing market. Structural wood panel products are more economical and efficient and can be stronger than traditional board sheathing. Structural wood panel products primarily include plywood and oriented strand board (OSB).

Key to Adjustment Factors:
Lumber strength is affected by the cumulative duration of maximum variable loads experienced during the life of the structure. In other words, strength is affected by both the load intensity and its duration (i.e., the load history). Because of its natural composition, wood is better able to resist higher short-term loads (i.e., transient live loads or impact loads) than long-term loads (i.e., dead loads and sustained live loads). Under impact loading, wood can resist about twice as much stress as the standard 10-year load duration (i.e., normal duration) to which wood bending stress properties are normalized in the NDS.
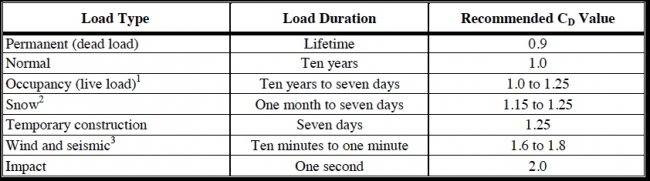
When other loads with different duration characteristics are considered, it is necessary to modify certain tabulated stresses by a load duration factor (CD) as shown in Table 5.3. Values of the load duration factor, CD, for various load types are based on the total accumulated time effects of a given type of load during the useful life of a structure. CD increases with decreasing load duration.
Where more than one load type is specified in a design analysis, the load duration factor associated with the shortest duration load is applied to the entire combination of loads.
The design of the above-grade structure involves the following structural systems and assemblies:
- floors;
- walls; and
- roofs.

Each system can be complex to design as a whole; therefore, simple analysis usually focuses on the individual elements that constitute the system. In some cases, “system effects” may be considered in simplified form and applied to the design of certain elements that constitute specifically defined systems.
Structural elements that make up a residential structural system include:
Let's look at the NDS equations in general, which includes design examples that detail the appropriate use of the equations for specific structural elements or systems in light, wood-framed construction, focusing primarily on framing with traditional dimensional lumber, giving some consideration to common engineered wood products. Other wood framing methods, such as post-and-beam construction, are not explicitly addressed here, although much of the information is relevant. However, system considerations and system factors presented here are only relevant to light, wood-framed construction using dimensional lumber.
Regardless of the type of structural element, the inspector must first determine nominal design loads. The loads acting on a framing member or system are usually calculated in accordance with the applicable provisions of the locally approved building code and engineering standards.
While prescriptive design tables or span tables and similar design aids commonly used in residential applications are not included herein, the inspector may save considerable effort by consulting such resources. Most local, state or national model building codes, such as The One- and Two-Family Dwelling Code (ICC), contain prescriptive design and construction provisions for conventional residential construction. For high-wind conditions, prescriptive guidelines for design and construction may be found in the Wood-Frame Construction Manual for One- and Two-Family Dwellings (AFPA). The inspector is also encouraged to obtain design data on a variety of proprietary engineered-wood products that are suitable for many special design needs in residential construction. However, these materials generally should not be viewed as simple one-to-one substitutes for conventional wood framing, and any special design and construction requirements should be carefully considered in accordance with the manufacturer’s recommendation or applicable code evaluation reports.
Material Properties
It is essential that a residential inspector specifying wood materials appreciate the natural characteristics of wood and their effect on the engineering properties of lumber. A brief discussion of the properties of lumber and structural wood panels follows.
Lumber
General
As with all materials, the inspector must consider wood’s strengths and weaknesses. A comprehensive source of technical information on the characteristics of wood is the Wood Engineering Handbook, Second Edition (Forest Products Laboratory). For the most part, the knowledge embodied in the handbook is reflected in the provisions of the NDS and the NDS Supplement (NDS-S) design data; however, many aspects of wood design require good judgment.
Wood is a natural substance that, as a structural material, demonstrates unique and complex characteristics. Wood’s structural properties can be traced back to its natural composition. Wood is foremost a non-homogeneous, non-isotropic material, and thus exhibits different structural properties, depending on the orientation of stresses relative to the grain of the wood. The grain is produced by the tree’s annual growth rings, which determine the properties of the wood along three orientations: tangential, radial and longitudinal.
Given that lumber is cut from logs in a longitudinal direction, the grain is parallel to the length of the lumber member. Depending on where the lumber is cut relative to the center of a log (i.e., tangential versus radial), properties vary across the width and thickness of an individual member.
Wood Species
Structural lumber can be manufactured from a variety of wood species; however, the various species used in a given locality are a function of the economy, regional availability, and required strength properties. A wood species is classified as either hardwood or softwood. Hardwoods are broad-leafed deciduous trees, while softwoods (i.e., conifers) are trees with needle-like leaves and are generally evergreen.
Most structural lumber is manufactured from softwoods because of the trees’ faster growth rate, availability, and workability (i.e., ease of cutting, nailing, etc.). A wood species is further classified into groups or combinations as defined in the NDS. Species within a group have similar properties and are subject to the same grading rules. Douglas fir-larch, southern yellow pine, hem-fir, and spruce-pine-fir are species groups that are widely used in residential applications in the United States.
Lumber Sizes
Wood members are referred to by nominal sizes (e.g., 2x4); however, true dimensions are somewhat less. The difference occurs during the dressing stage of the lumber process, when each surface of the member is planed to its final dressed dimension after shrinkage has occurred as a result of the drying or seasoning process. Generally, there is a 1/4- to 3/4-inch difference between the nominal and dressed sizes of dry-sawn lumber (refer to NDS-S Table 1B for specific dimensions). For example, a 2x4 is actually 1.5 inches by 3.5 inches, a 2x10 is 1.5 inches by 9.25 inches, and a 1x4 is 3/4-inch by 3.5 inches. This guide uses nominal member size, but it is important to note that the inspector must apply the actual dimensions of the lumber when analyzing structural performance or detailing construction dimensions.
Based on the expected application, the tabulated values in the NDS are classified by the species of wood as well as by the nominal size of a member.
- bending members;
- columns;
- combined bending and axial loaded members;
- sheathing (i.e., diaphragm); and
- connections.
Let's look at the NDS equations in general, which includes design examples that detail the appropriate use of the equations for specific structural elements or systems in light, wood-framed construction, focusing primarily on framing with traditional dimensional lumber, giving some consideration to common engineered wood products. Other wood framing methods, such as post-and-beam construction, are not explicitly addressed here, although much of the information is relevant. However, system considerations and system factors presented here are only relevant to light, wood-framed construction using dimensional lumber.
Regardless of the type of structural element, the inspector must first determine nominal design loads. The loads acting on a framing member or system are usually calculated in accordance with the applicable provisions of the locally approved building code and engineering standards.
While prescriptive design tables or span tables and similar design aids commonly used in residential applications are not included herein, the inspector may save considerable effort by consulting such resources. Most local, state or national model building codes, such as The One- and Two-Family Dwelling Code (ICC), contain prescriptive design and construction provisions for conventional residential construction. For high-wind conditions, prescriptive guidelines for design and construction may be found in the Wood-Frame Construction Manual for One- and Two-Family Dwellings (AFPA). The inspector is also encouraged to obtain design data on a variety of proprietary engineered-wood products that are suitable for many special design needs in residential construction. However, these materials generally should not be viewed as simple one-to-one substitutes for conventional wood framing, and any special design and construction requirements should be carefully considered in accordance with the manufacturer’s recommendation or applicable code evaluation reports.
Material Properties
It is essential that a residential inspector specifying wood materials appreciate the natural characteristics of wood and their effect on the engineering properties of lumber. A brief discussion of the properties of lumber and structural wood panels follows.
Lumber
General
As with all materials, the inspector must consider wood’s strengths and weaknesses. A comprehensive source of technical information on the characteristics of wood is the Wood Engineering Handbook, Second Edition (Forest Products Laboratory). For the most part, the knowledge embodied in the handbook is reflected in the provisions of the NDS and the NDS Supplement (NDS-S) design data; however, many aspects of wood design require good judgment.
Wood is a natural substance that, as a structural material, demonstrates unique and complex characteristics. Wood’s structural properties can be traced back to its natural composition. Wood is foremost a non-homogeneous, non-isotropic material, and thus exhibits different structural properties, depending on the orientation of stresses relative to the grain of the wood. The grain is produced by the tree’s annual growth rings, which determine the properties of the wood along three orientations: tangential, radial and longitudinal.
Given that lumber is cut from logs in a longitudinal direction, the grain is parallel to the length of the lumber member. Depending on where the lumber is cut relative to the center of a log (i.e., tangential versus radial), properties vary across the width and thickness of an individual member.
Wood Species
Structural lumber can be manufactured from a variety of wood species; however, the various species used in a given locality are a function of the economy, regional availability, and required strength properties. A wood species is classified as either hardwood or softwood. Hardwoods are broad-leafed deciduous trees, while softwoods (i.e., conifers) are trees with needle-like leaves and are generally evergreen.
Most structural lumber is manufactured from softwoods because of the trees’ faster growth rate, availability, and workability (i.e., ease of cutting, nailing, etc.). A wood species is further classified into groups or combinations as defined in the NDS. Species within a group have similar properties and are subject to the same grading rules. Douglas fir-larch, southern yellow pine, hem-fir, and spruce-pine-fir are species groups that are widely used in residential applications in the United States.
Lumber Sizes
Wood members are referred to by nominal sizes (e.g., 2x4); however, true dimensions are somewhat less. The difference occurs during the dressing stage of the lumber process, when each surface of the member is planed to its final dressed dimension after shrinkage has occurred as a result of the drying or seasoning process. Generally, there is a 1/4- to 3/4-inch difference between the nominal and dressed sizes of dry-sawn lumber (refer to NDS-S Table 1B for specific dimensions). For example, a 2x4 is actually 1.5 inches by 3.5 inches, a 2x10 is 1.5 inches by 9.25 inches, and a 1x4 is 3/4-inch by 3.5 inches. This guide uses nominal member size, but it is important to note that the inspector must apply the actual dimensions of the lumber when analyzing structural performance or detailing construction dimensions.
Based on the expected application, the tabulated values in the NDS are classified by the species of wood as well as by the nominal size of a member.
Typical NDS classifications follow:
Lumber Grades
Lumber is graded in accordance with standardized grading rules that consider the effect of natural growth characteristics and defects, such as knots and angle of grain, on the member’s structural properties. Growth characteristics reduce the overall strength of the member relative to a “perfect,” clear-grained member without any natural defects. Most lumber is visually graded, although it can also be machine stress-rated or machine-evaluated.
Visually graded lumber is graded by an individual who examines the wood member at the mill in accordance with an approved agency’s grading rules. The grader separates wood members into the appropriate grade classes. Typical visual grading classes, in order of decreasing strength properties, are Select Structural, No. 1, No. 2, Stud, etc. Refer to the NDS Supplement (NDS-S) for more information on grades of different species of lumber. The inspector should consult a lumber supplier or contractor regarding locally available lumber species and grades.
Machine stress-rated (MSR) and machine-evaluated lumber (MEL) are subjected to non-destructive testing of each piece. The wood member is then marked with the appropriate grade stamp, which includes the allowable bending stress (Fb) and the modulus of elasticity (E). This grading method yields lumber with more consistent structural properties than visual grading only.
While grading rules vary among grading agencies, the U.S. Department of Commerce has set forth minimums for voluntary adoption by the recognized lumber grading agencies. For more information regarding grading rules, refer to the American Softwood Lumber Voluntary Product Standard, which is maintained by the National Institute for Standards and Technology (NIST). NDS-S lists approved grading agencies and roles.
Moisture Content
Wood properties and dimensions change with moisture content (MC). Living wood contains a considerable amount of free and bound water. Free water is contained between the wood cells and is the first water to be driven off in the drying process. Its loss affects neither volume nor structural properties. Bound water is contained within the wood cells and accounts for most of the moisture under 30%; its loss results in changes in both volume (i.e., shrinkage) and structural properties. The strength of wood peaks at about 10 to 15% MC.
Given that wood generally has an MC of more than 30% when cut and may dry to an equilibrium moisture content (EMC) of 8 to 10% in a protected environment, it should be sufficiently dried or seasoned before installation. Proper drying and storage of lumber minimizes problems associated with lumber shrinkage and warping. A minimum recommendation calls for using surface-dry lumber with a maximum 19% MC. In uses where shrinkage is critical, specifications may call for KD-15, which is kiln-dried lumber with a maximum moisture content of 15%. The tabulated design values in the NDS are based on a moisture content of 19% for dimensional lumber.
The inspector should plan for the vertical movement that may occur in a structure as a result of shrinkage. For more complicated structural details that call for various types of materials and systems, the inspector might have to account for differential shrinkage by isolating members that will shrink from those that will maintain dimensional stability. The inspector should also detail the structure such that shrinkage is as uniform as possible, thereby minimizing shrinkage effects on finish surfaces. When practical, details that minimize the amount of wood transferring loads perpendicular-to-grain are preferable.
Shrinking and swelling can be estimated for the width and thickness of wood members (i.e., tangentially and radially, with respect to annual rings). Shrinkage in the longitudinal direction of a wood member (parallel to the grain) is negligible.
Durability
Moisture is a primary factor affecting the durability of lumber. Fungi, which feed on wood cells, require moisture, air, and favorable temperatures to survive. When wood is subject to moisture levels above 20% and other favorable conditions, decay begins to set in.
- Boards are less than 2 inches thick.
- Dimensional lumber is a minimum of 2 inches wide and 2 to 4 inches thick.
- Beams and stringers are a minimum of 5 inches thick, with the width at least 2 inches greater than the thickness dimension.
- Posts and timbers are a minimum of 5 inches thick, and the width does not exceed the thickness by more than 2 inches.
- Decking is 2 to 4 inches thick and loaded in the weak axis of bending for a roof, floor or wall surface.
Lumber Grades
Lumber is graded in accordance with standardized grading rules that consider the effect of natural growth characteristics and defects, such as knots and angle of grain, on the member’s structural properties. Growth characteristics reduce the overall strength of the member relative to a “perfect,” clear-grained member without any natural defects. Most lumber is visually graded, although it can also be machine stress-rated or machine-evaluated.
Visually graded lumber is graded by an individual who examines the wood member at the mill in accordance with an approved agency’s grading rules. The grader separates wood members into the appropriate grade classes. Typical visual grading classes, in order of decreasing strength properties, are Select Structural, No. 1, No. 2, Stud, etc. Refer to the NDS Supplement (NDS-S) for more information on grades of different species of lumber. The inspector should consult a lumber supplier or contractor regarding locally available lumber species and grades.
Machine stress-rated (MSR) and machine-evaluated lumber (MEL) are subjected to non-destructive testing of each piece. The wood member is then marked with the appropriate grade stamp, which includes the allowable bending stress (Fb) and the modulus of elasticity (E). This grading method yields lumber with more consistent structural properties than visual grading only.
While grading rules vary among grading agencies, the U.S. Department of Commerce has set forth minimums for voluntary adoption by the recognized lumber grading agencies. For more information regarding grading rules, refer to the American Softwood Lumber Voluntary Product Standard, which is maintained by the National Institute for Standards and Technology (NIST). NDS-S lists approved grading agencies and roles.
Moisture Content
Wood properties and dimensions change with moisture content (MC). Living wood contains a considerable amount of free and bound water. Free water is contained between the wood cells and is the first water to be driven off in the drying process. Its loss affects neither volume nor structural properties. Bound water is contained within the wood cells and accounts for most of the moisture under 30%; its loss results in changes in both volume (i.e., shrinkage) and structural properties. The strength of wood peaks at about 10 to 15% MC.
Given that wood generally has an MC of more than 30% when cut and may dry to an equilibrium moisture content (EMC) of 8 to 10% in a protected environment, it should be sufficiently dried or seasoned before installation. Proper drying and storage of lumber minimizes problems associated with lumber shrinkage and warping. A minimum recommendation calls for using surface-dry lumber with a maximum 19% MC. In uses where shrinkage is critical, specifications may call for KD-15, which is kiln-dried lumber with a maximum moisture content of 15%. The tabulated design values in the NDS are based on a moisture content of 19% for dimensional lumber.
The inspector should plan for the vertical movement that may occur in a structure as a result of shrinkage. For more complicated structural details that call for various types of materials and systems, the inspector might have to account for differential shrinkage by isolating members that will shrink from those that will maintain dimensional stability. The inspector should also detail the structure such that shrinkage is as uniform as possible, thereby minimizing shrinkage effects on finish surfaces. When practical, details that minimize the amount of wood transferring loads perpendicular-to-grain are preferable.
Shrinking and swelling can be estimated for the width and thickness of wood members (i.e., tangentially and radially, with respect to annual rings). Shrinkage in the longitudinal direction of a wood member (parallel to the grain) is negligible.
Durability
Moisture is a primary factor affecting the durability of lumber. Fungi, which feed on wood cells, require moisture, air, and favorable temperatures to survive. When wood is subject to moisture levels above 20% and other favorable conditions, decay begins to set in.
Therefore, it is important to protect wood materials from moisture, by:
• limiting end use (e.g., specifying interior applications or isolating lumber from ground contact);
• using a weather barrier (e.g., siding, roofing, building wrap, flashing, etc.);
• applying a protective coating (e.g., paint, water repellent, etc.);
• installing roof overhangs and gutters; and
• specifying preservative-treated or naturally decay-resistant wood.
For homes, an exterior weather barrier (e.g., roofing and siding) protects most structural wood. However, improper detailing can lead to moisture intrusion and decay. Problems are commonly associated with improper or missing flashing and undue reliance on caulking to prevent moisture intrusion. For additional information and guidance on improving the durability of wood in buildings, refer to Prevention and Control of Decay in Homes (HUD).
• limiting end use (e.g., specifying interior applications or isolating lumber from ground contact);
• using a weather barrier (e.g., siding, roofing, building wrap, flashing, etc.);
• applying a protective coating (e.g., paint, water repellent, etc.);
• installing roof overhangs and gutters; and
• specifying preservative-treated or naturally decay-resistant wood.
For homes, an exterior weather barrier (e.g., roofing and siding) protects most structural wood. However, improper detailing can lead to moisture intrusion and decay. Problems are commonly associated with improper or missing flashing and undue reliance on caulking to prevent moisture intrusion. For additional information and guidance on improving the durability of wood in buildings, refer to Prevention and Control of Decay in Homes (HUD).

Wood members that are in contact with the ground should be preservative-treated. The most common lumber treatment is CCA (copper chromium arsenate), which should be used for applications such as sill plates located near the ground and for exterior decks. It is important to specify the correct level of treatment: 0.4 pcf retention for non-ground-contact exterior exposure, and 0.6 pcf for ground contact.
Termites and other wood-destroying insects (e.g., carpenter ants, boring beetles, etc.) attack wood materials. Some practical solutions include: the chemical treatment of soil; the installation of physical barriers (e.g., termite shields); and the specification of treated lumber.
Termites are a special problem in warmer climates, although they also plague many other areas of the United States. The most common termites are subterranean termites that nest in the ground and enter wood that is near or in contact with damp soil. They gain access to above-grade wood through cracks in the foundation or through shelter tubes (mud tunnels) on the surface of foundation walls. Since the presence of termites lends itself to visual detection, wood-framed homes require periodic inspection for signs of termites.
Structural Wood Panels
Historically, boards were used for roof, floor, and wall sheathing; in the last 30 years, however, structural wood panel products have come to dominate the sheathing market. Structural wood panel products are more economical and efficient and can be stronger than traditional board sheathing. Structural wood panel products primarily include plywood and oriented strand board (OSB).

Plywood is manufactured from wood veneers glued together under high temperature and pressure. Each veneer or ply is placed with its grain perpendicular to the grain of the previous layer. The outer layers are placed with their grain parallel to the longer dimension of the panel. Thus, plywood is stronger in bending along the long direction and should be placed with the long dimension spanning floor and roof framing members. The number of plies typically ranges from three to five. Oriented strand board is manufactured from thin wood strands glued together under high temperature and pressure. The strands are layered and oriented to produce strength properties similar to plywood; therefore, the material is used for the same applications as plywood.
The inspector should specify the grade and span rating of structural wood panels to meet the required application and loading condition (i.e., roof, wall or floor). The most common panel size is 4x8-foot panels, with thicknesses typically ranging from 3/8-inch to more than 1 inch. Panels can be ordered in longer lengths for special applications.
Plywood is performance-rated for industrial and construction plywood. OSB products are performance-rated. However, these standards are voluntary, and not all wood-based panel products are rated accordingly. The rating system of the APA-Engineered Wood Association (formerly the American Plywood Association) for structural wood panel sheathing products and those used by other structural panel trademarking organizations are based on the U.S. Department of Commerce's voluntary product standards.
The veneer grade of plywood is associated with the veneers used on the exposed faces of a panel as follows:
Lumber Design Values
The NDS-S provides tabulated design stress values for bending, tension parallel to grain, shear parallel to grain, compression parallel and perpendicular to grain, and modulus of elasticity. In particular, NDS includes the most up-to-date design values based on test results from an eight-year, full-scale testing program that used lumber samples from mills across the United States and Canada.
Characteristic structural properties for use in allowable stress design and load and resistance factor design are used to establish design values. Test data collected in accordance with the applicable standards determine a characteristic strength value for each grade and species of lumber. The value is usually the mean (average) or 5th-percentile test value. The 5th percentile represents the value that 95% of the sampled members exceeded. In ASD, characteristic structural values are multiplied by the reduction factors in Table 5.1. The reduction factors are implicit in the allowable values published in the NDS-S for standardized conditions. The reduction factor normalizes the lumber properties to a standard set of conditions related to load duration, moisture content, and other factors. It also includes a safety adjustment (if applicable) to the particular limit state (i.e., ultimate capacity). Therefore, for specific design conditions that differ from the standard basis, design property values should be adjusted.
The reduction factors in Table 5.1 are derived as follows, as reported in ASTM D2915 (ASTM):
The allowable values published in the NDS-S are determined for a standard set of conditions. Yet, given the many variations in the characteristics of wood that affect the material’s structural properties, several adjustment factors are available to modify the published values. For efficient design, it is important to use the appropriate adjustments for conditions that vary from those used to derive the standard design values. Table 5.2 presents adjustment factors that apply to different structural properties of wood.
TABLE 5.1 Design Properties and Associated Reduction Factors for ASD

TABLE 5.2 Adjustment Factor Applicability to Design Values for Wood

Plywood is performance-rated for industrial and construction plywood. OSB products are performance-rated. However, these standards are voluntary, and not all wood-based panel products are rated accordingly. The rating system of the APA-Engineered Wood Association (formerly the American Plywood Association) for structural wood panel sheathing products and those used by other structural panel trademarking organizations are based on the U.S. Department of Commerce's voluntary product standards.
The veneer grade of plywood is associated with the veneers used on the exposed faces of a panel as follows:
- Grade A: the highest-quality veneer grade, which is intended for cabinet or furniture use;
- Grade B: a high-quality veneer grade, which is intended for cabinet or furniture use, with all defects repaired;
- Grade C: the minimum veneer grade, which is intended for exterior use; and
- Grade D: the lowest-quality veneer grade, which is intended for interior use or where protected from exposure to weather.
- Exterior panels are designed for applications with permanent exposure to the weather or moisture.
- Exposure 1 panels are designed for applications where temporary exposure to the weather due to construction sequence may be expected.
- Exposure 2 panels are designed for applications with a potential for high humidity or wetting, but are generally protected during construction.
- Interior panels are designed for interior applications only.
Lumber Design Values
The NDS-S provides tabulated design stress values for bending, tension parallel to grain, shear parallel to grain, compression parallel and perpendicular to grain, and modulus of elasticity. In particular, NDS includes the most up-to-date design values based on test results from an eight-year, full-scale testing program that used lumber samples from mills across the United States and Canada.
Characteristic structural properties for use in allowable stress design and load and resistance factor design are used to establish design values. Test data collected in accordance with the applicable standards determine a characteristic strength value for each grade and species of lumber. The value is usually the mean (average) or 5th-percentile test value. The 5th percentile represents the value that 95% of the sampled members exceeded. In ASD, characteristic structural values are multiplied by the reduction factors in Table 5.1. The reduction factors are implicit in the allowable values published in the NDS-S for standardized conditions. The reduction factor normalizes the lumber properties to a standard set of conditions related to load duration, moisture content, and other factors. It also includes a safety adjustment (if applicable) to the particular limit state (i.e., ultimate capacity). Therefore, for specific design conditions that differ from the standard basis, design property values should be adjusted.
The reduction factors in Table 5.1 are derived as follows, as reported in ASTM D2915 (ASTM):
- Fb reduction factor = (10/16 load-duration factor)(10/13 safety factor);
- Ft reduction factor = (10/16 load-duration factor)(10/13 safety factor);
- Fv reduction factor = (10/16 load-duration factor)(4/9 stress-concentration factor)(8/9 safety factor);
- Fc reduction factor = (2/3 load-duration factor)(4/5 safety factor); and
- Fc⊥ reduction factor = (2/3 end-position factor).
Adjustment Factors
The allowable values published in the NDS-S are determined for a standard set of conditions. Yet, given the many variations in the characteristics of wood that affect the material’s structural properties, several adjustment factors are available to modify the published values. For efficient design, it is important to use the appropriate adjustments for conditions that vary from those used to derive the standard design values. Table 5.2 presents adjustment factors that apply to different structural properties of wood.
TABLE 5.1 Design Properties and Associated Reduction Factors for ASD

TABLE 5.2 Adjustment Factor Applicability to Design Values for Wood

Key to Adjustment Factors:
- CD, Load Duration Factor, applies when loads are other than the normal 10-year duration.
- Cr, Repetitive Member Factor, applies to bending members in assemblies with multiple members spaced at maximum 24 inches on center.
- CH, Horizontal Shear Factor, applies to individual or multiple members with regard to horizontal, parallel-to-grain splitting.
- CF, Size Factor, applies to member sizes/grades other than standard test specimens, but does not apply to southern yellow pine.
- CP, Column Stability Factor, applies to lateral support condition of compression members.
- CL, Beam Stability Factor, applies to bending members not subject to continuous lateral support on the compression edge.
- CM, Wet Service Factor, applies where the moisture content is expected to exceed 19% for extended periods.
- Cfu, Flat Use Factor, applies where dimensional lumber 2 to 4 inches thick is subject to a bending load in its weak axis direction.
- Cb, Bearing Area Factor, applies to members with bearing less than 6 inches and not nearer than 3 inches from the members’ ends.
- CT, Buckling Stiffness Factor, applies only to maximum 2x4 dimensional lumber in the top chord of wood trusses that are subjected to combined flexure and axial compression.
- CV, Volume Factor, applies to Glulam® bending members loaded perpendicular to the wide face of the laminations in strong axis bending.
- Ct, Temperature Factor, applies where temperatures exceed 100° F for long periods; not normally required when wood members are subjected to intermittent higher temperatures, such as in roof structures.
- Ci, Incising Factor, applies where structural-sawn lumber is incised to increase penetration of preservatives with small incisions cut parallel to the grain.
- Cc, Curvature Factor, applies only to curved portions of glued, laminated bending members.
- Cf, Form Factor, applies where bending members are either round or square with diagonal loading.
Lumber strength is affected by the cumulative duration of maximum variable loads experienced during the life of the structure. In other words, strength is affected by both the load intensity and its duration (i.e., the load history). Because of its natural composition, wood is better able to resist higher short-term loads (i.e., transient live loads or impact loads) than long-term loads (i.e., dead loads and sustained live loads). Under impact loading, wood can resist about twice as much stress as the standard 10-year load duration (i.e., normal duration) to which wood bending stress properties are normalized in the NDS.
When other loads with different duration characteristics are considered, it is necessary to modify certain tabulated stresses by a load duration factor (CD) as shown in Table 5.3. Values of the load duration factor, CD, for various load types are based on the total accumulated time effects of a given type of load during the useful life of a structure. CD increases with decreasing load duration.
Where more than one load type is specified in a design analysis, the load duration factor associated with the shortest duration load is applied to the entire combination of loads.
For example, for the load combination, Dead Load + Snow Load + Wind Load, the load duration factor, CD, is equal to 1.6.
TABLE 5.3 Recommended Load Duration Factors for ASD
Repetitive Member Factor (Cr)
When three or more parallel dimensional lumber members are spaced a maximum of 24 inches on center and connected with structural sheathing, they comprise a structural system with more bending capacity than the sum of the single members acting individually. Therefore, most elements in a house structure benefit from an adjustment for the system strength effects inherent in repetitive members.
The tabulated design values given in the NDS are based on single members; thus, an increase in allowable stress is permitted in order to account for repetitive members. While the NDS recommends a repetitive member factor of 1.15 or a 15% increase in bending strength, system assembly tests have demonstrated that the NDS repetitive member factor is conservative for certain conditions. In fact, test results from several studies support the range of repetitive member factors shown in Table 5.4 for certain design applications. As shown in Table 5.2, the adjustment factor applies only to extreme fiber in bending, Fb.
TABLE 5.4 Recommended Repetitive Member Factors for Dimension Lumber Used in Framing Systems

With the exception of the 1.15 repetitive member factor, the NDS does not currently recognize the values in Table 5.4. Therefore, the values in Table 5.4 are provided for use by the inspector as an alternative method based on various sources of technical information, including certain standards, code recognized guidelines, and research studies.
Horizontal Shear Factor (CH)
Given that lumber does not dry uniformly, it is subject to warping, checking and splitting, all of which reduce the strength of a member. The horizontal stress values in the NDS-S conservatively account for any checks and splits that may form during the seasoning process and, as in the worst-case values, assume substantial horizontal splits in all wood members. Although a horizontal split may occur in some members, all members in a repetitive member system rarely experience such splits. Therefore, a CH of greater than 1 should typically apply when repetitive framing or built-up members are used. For members with no splits, CH equals 2.
In addition, future allowable horizontal shear values will be increased by a factor of 2 or more because of a recent change in the applicable standard regarding assignment of strength properties. The change is a result of removing a conservative adjustment to the test data whereby a 50% reduction for checks and splits was applied in addition to a 4/9 stress concentration factor, as described in Section 5.2.3. As an interim solution, a shear adjustment factor, CH, of 2 should therefore apply to all designs that use horizontal shear values in 1997 and earlier editions of the NDS. As shown in Table 5.2, the CH factor applies only to the allowable horizontal shear stress, Fv. As an interim consideration regarding horizontal shear at notches and connections in members, a CH value of 1.5 is recommended for use with provisions in NDS•3.4.4 and 3.4.5 for dimensional lumber only.
Size Factor (CF)
Tabulated design values in the NDS-S are based on testing conducted on members of certain sizes. The specified depth for dimensional lumber members subjected to testing is 12 inches for No. 3 or better, 6 inches for stud-grade members, and 4 inches for construction-, standard- or utility-grade members (i.e., CF=1.0).
The size of a member affects unit strength because of the member’s relationship to the likelihood of naturally occurring defects in the material. Therefore, an adjustment to certain tabulated values is appropriate for sizes other than those tested; however, the tabulated values for southern yellow pine have already been adjusted for size and do not require application of CF. Table 5.2 indicates the tabulated values that should be adjusted to account for size differences. The adjustment applies when visually graded lumber is 2 to 4 inches thick or when a minimum 5-inch-thick rectangular bending member exceeds 12 inches in depth. Refer to NDS-S for the appropriate size adjustment factor.
Column Stability Factor (CP)
Tabulated compression design values in the NDS-S are based on the assumption that a compression member is continuously supported along its length to prevent lateral displacement in both the weak and strong axes. When a compression member is subject to continuous lateral support in at least two orthogonal directions, Euler buckling cannot occur. However, many compression members (e.g., interior columns or wall framing) do not have continuous lateral support in two directions.
The column stability factor, CP, adjusts the tabulated compression stresses to account for the possibility of column buckling. For rectangular or non-symmetric columns, CP must be determined for both the weak- and strong-axis bracing conditions. CP is based on end-fixity, effective length of the member between lateral braces, and the cross-sectional dimensions of the member that affect the slenderness ratio used in calculating the critical buckling stress. Given that the Euler buckling effect is associated only with axial loads, the CP factor applies to the allowable compressive stress parallel to grain, Fc, as shown in Table 5.2.
Beam Stability Factor (CL)
The tabulated bending design values, Fb, given in the NDS-S are applicable to bending members that are either braced against lateral-torsional buckling (i.e., twisting) or stable without bracing (i.e., the depth is no greater than the breadth of the member). Most bending members in residential construction are laterally supported on the compression edge by some type of sheathing product. The beam stability factor does, however, apply to conditions such as ceiling joists supporting unfinished attic space. When a member does not meet the lateral support requirements of NDS 3.3.3 or the stability requirements of NDS 4.4.1, the inspector should modify the tabulated bending design values by using the beam stability factor, CL, to account for the possibility of lateral-torsional buckling. For glued laminated timber bending members, the volume factor (CV) and beam stability factor (CL) are not applied simultaneously; thus, the lesser of these factors applies. Refer to the NDS 3.3.3 for the equations used to calculate CL.
Structural Evaluation
TABLE 5.3 Recommended Load Duration Factors for ASD

Repetitive Member Factor (Cr)
When three or more parallel dimensional lumber members are spaced a maximum of 24 inches on center and connected with structural sheathing, they comprise a structural system with more bending capacity than the sum of the single members acting individually. Therefore, most elements in a house structure benefit from an adjustment for the system strength effects inherent in repetitive members.
The tabulated design values given in the NDS are based on single members; thus, an increase in allowable stress is permitted in order to account for repetitive members. While the NDS recommends a repetitive member factor of 1.15 or a 15% increase in bending strength, system assembly tests have demonstrated that the NDS repetitive member factor is conservative for certain conditions. In fact, test results from several studies support the range of repetitive member factors shown in Table 5.4 for certain design applications. As shown in Table 5.2, the adjustment factor applies only to extreme fiber in bending, Fb.
TABLE 5.4 Recommended Repetitive Member Factors for Dimension Lumber Used in Framing Systems

With the exception of the 1.15 repetitive member factor, the NDS does not currently recognize the values in Table 5.4. Therefore, the values in Table 5.4 are provided for use by the inspector as an alternative method based on various sources of technical information, including certain standards, code recognized guidelines, and research studies.
Horizontal Shear Factor (CH)
Given that lumber does not dry uniformly, it is subject to warping, checking and splitting, all of which reduce the strength of a member. The horizontal stress values in the NDS-S conservatively account for any checks and splits that may form during the seasoning process and, as in the worst-case values, assume substantial horizontal splits in all wood members. Although a horizontal split may occur in some members, all members in a repetitive member system rarely experience such splits. Therefore, a CH of greater than 1 should typically apply when repetitive framing or built-up members are used. For members with no splits, CH equals 2.
In addition, future allowable horizontal shear values will be increased by a factor of 2 or more because of a recent change in the applicable standard regarding assignment of strength properties. The change is a result of removing a conservative adjustment to the test data whereby a 50% reduction for checks and splits was applied in addition to a 4/9 stress concentration factor, as described in Section 5.2.3. As an interim solution, a shear adjustment factor, CH, of 2 should therefore apply to all designs that use horizontal shear values in 1997 and earlier editions of the NDS. As shown in Table 5.2, the CH factor applies only to the allowable horizontal shear stress, Fv. As an interim consideration regarding horizontal shear at notches and connections in members, a CH value of 1.5 is recommended for use with provisions in NDS•3.4.4 and 3.4.5 for dimensional lumber only.
Size Factor (CF)
Tabulated design values in the NDS-S are based on testing conducted on members of certain sizes. The specified depth for dimensional lumber members subjected to testing is 12 inches for No. 3 or better, 6 inches for stud-grade members, and 4 inches for construction-, standard- or utility-grade members (i.e., CF=1.0).
The size of a member affects unit strength because of the member’s relationship to the likelihood of naturally occurring defects in the material. Therefore, an adjustment to certain tabulated values is appropriate for sizes other than those tested; however, the tabulated values for southern yellow pine have already been adjusted for size and do not require application of CF. Table 5.2 indicates the tabulated values that should be adjusted to account for size differences. The adjustment applies when visually graded lumber is 2 to 4 inches thick or when a minimum 5-inch-thick rectangular bending member exceeds 12 inches in depth. Refer to NDS-S for the appropriate size adjustment factor.
Column Stability Factor (CP)
Tabulated compression design values in the NDS-S are based on the assumption that a compression member is continuously supported along its length to prevent lateral displacement in both the weak and strong axes. When a compression member is subject to continuous lateral support in at least two orthogonal directions, Euler buckling cannot occur. However, many compression members (e.g., interior columns or wall framing) do not have continuous lateral support in two directions.
The column stability factor, CP, adjusts the tabulated compression stresses to account for the possibility of column buckling. For rectangular or non-symmetric columns, CP must be determined for both the weak- and strong-axis bracing conditions. CP is based on end-fixity, effective length of the member between lateral braces, and the cross-sectional dimensions of the member that affect the slenderness ratio used in calculating the critical buckling stress. Given that the Euler buckling effect is associated only with axial loads, the CP factor applies to the allowable compressive stress parallel to grain, Fc, as shown in Table 5.2.
Beam Stability Factor (CL)
The tabulated bending design values, Fb, given in the NDS-S are applicable to bending members that are either braced against lateral-torsional buckling (i.e., twisting) or stable without bracing (i.e., the depth is no greater than the breadth of the member). Most bending members in residential construction are laterally supported on the compression edge by some type of sheathing product. The beam stability factor does, however, apply to conditions such as ceiling joists supporting unfinished attic space. When a member does not meet the lateral support requirements of NDS 3.3.3 or the stability requirements of NDS 4.4.1, the inspector should modify the tabulated bending design values by using the beam stability factor, CL, to account for the possibility of lateral-torsional buckling. For glued laminated timber bending members, the volume factor (CV) and beam stability factor (CL) are not applied simultaneously; thus, the lesser of these factors applies. Refer to the NDS 3.3.3 for the equations used to calculate CL.
Structural Evaluation
As with any structural design, the inspector should perform several checks with respect to various design factors. This section provides an overview of checks specified in the NDS and specifies several design concerns that are not addressed by the NDS. In general, the two categories of structural design concerns are:
• Structural Safety (strength)
• Structural Safety (strength)
◦ Bending and lateral stability
◦ Horizontal shear
◦ Bearing
◦ Combined bending and axial loading
◦ Compression and column stability
◦ Tension
• Structural Serviceability
◦ Deflection due to bending
◦ Floor vibration
◦ Shrinkage
Structural Safety Checks
Bending (Flexural) Capacity
The following equations from the NDS determine if a member has sufficient bending strength. Notches in bending members should be avoided, but small notches are permissible; refer to NDS 3.2.3. Similarly, the diameter of holes in bending members should not exceed one-third the member’s depth and should be located along the centerline of the member. Greater flexural capacity may be obtained by increasing member depth, decreasing the clear span or spacing of the member, or selecting a grade and species of lumber with a higher allowable bending stress. Engineered wood products or alternative materials may also be considered.

Horizontal Shear
Because shear parallel to grain (i.e., horizontal shear) is induced by bending action, it is also known as bending shear and is greatest at the neutral axis. Bending shear is not transverse shear; lumber will always fail in other modes before failing in transverse or cross-grain shear owing to the longitudinal orientation of the wood fibers in structural members.
The horizontal shear force is calculated for solid-sawn lumber by including the component of all loads (uniform and concentrated) that act perpendicular to the bearing surface of the solid member in accordance with NDS 3.4.3. Loads within a distance, d, from the bearing point are not included in the horizontal shear calculation; d is the depth of the member for solid rectangular members. Transverse shear is not a required design check, although it is used to determine the magnitude of horizontal shear by using basic concepts of engineering mechanics as discussed below.
The following equations from NDS 3.4 for horizontal shear analysis are limited to solid flexural members, such as solid-sawn lumber, Glulam®, or mechanically laminated beams. Notches in beams can reduce shear capacity and should be considered in accordance with NDS 3.4.4. Also, bolted connections influence the shear capacity of a beam; refer to NDS 3.4.5. If required, greater horizontal shear capacity may be obtained by increasing member depth or width, decreasing the clear span or spacing of the member, or selecting another species with a higher allowable shear capacity. The general equation for horizontal shear stress is discussed in the NDS and in mechanics of materials textbooks. Because dimensional lumber is solid and rectangular, the simple equation for fv is most commonly used.

Compression Perpendicular to Grain (Bearing)
For bending members bearing on wood or metal, a minimum bearing of 1.5 inches is typically recommended. For bending members bearing on masonry, a minimum bearing of 3 inches is typically advised. The resulting bearing areas may not, however, be adequate in the case of heavily loaded members. On the other hand, they may be too conservative in the case of lightly loaded members. The minimum bearing lengths are considered to represent good practice.
The following equations from the NDS are based on net bearing area. Note that the provisions of the NDS acknowledge that the inner bearing edge experiences added pressure as the member bends. As a practical matter, the added pressure does not pose a problem because the compressive capacity, Fc⊥, of wood increases as the material is compressed. Further, the design value is based on a deformation limit, not on failure by crushing. Thus, the NDS recommends the added pressure at bearing edges not be considered. The inspector is also alerted to the use of the bearing area factor, Cb, which accounts for the ability of wood to distribute large stresses originating from a small bearing area not located near the end of a member. Examples include interior bearing supports and compressive loads on washers in bolted connections.

The above equations pertain to bearing that is perpendicular to grain; for bearing at an angle to grain, refer to NDS 3.10. The later condition would apply to sloped bending members (i.e., rafters) notched at an angle for bearing. For light-frame construction, bearing stress is rarely a limiting factor.
Combined Bending and Axial Loading
Depending on the application and the combination of loads considered, some members, such as wall studs and roof truss members, experience bending stress in addition to axial loading. The inspector should evaluate combined bending and axial stresses as appropriate. If additional capacity is required, the selection of a higher grade of lumber is not always an efficient solution for over-stressed compression members under combined axial and bending loads because the design may be limited by stability rather than by a stress failure mode. Efficiency issues will become evident when the inspector calculates the components of the combined stress interaction equations that are given below and found in the NDS.

Compression and Column Stability
For framing members that support axial loads only (i.e., columns), the inspector must consider whether the framing member can withstand the axial compressive forces on it without buckling or compressive failure. If additional compression strength is required, the inspector should increase member size, decrease framing member spacing, provide additional lateral support, or select a different grade and species of lumber with higher allowable stresses. Improving lateral support is usually the most efficient solution when stability controls the design (disregarding any architectural limitations). The need for improved lateral support will become evident when the inspector performs the calculations necessary to determine the stability factor, CP, in accordance with NDS 3.7. When a column has continuous lateral support in two directions, buckling is not an issue and CP = 1.0. If, however, the column is free to buckle in one or more directions, CP must be evaluated for each direction of possible buckling. The evaluation must also consider the spacing of intermediate bracing, if any, in each direction.

Tension
Relatively few members in light-frame construction resist tension forces only. One notable exception occurs in roof framing where cross-ties or bottom chords in trusses primarily resist tension forces. Other examples include chord and collector members in shear walls and horizontal diaphragms. Another possibility is a member subject to excessive uplift loads, such as those produced by extreme wind. In any event, connection design is usually the limiting factor in designing the transfer of tension forces in light-frame construction. Tension stresses in wood members are checked by using the equations below in accordance with NDS 3.8.

The NDS does not provide explicit methods for evaluating cross-grain tension forces and generally recommends the avoidance of cross-grain tension in lumber even though the material is capable of resisting limited cross-grain stresses. Design values for cross-grain tension may be approximated by using one-third of the unadjusted horizontal shear stress value Fv. One application of cross-grain tension in design is in the transfer of moderate uplift loads from wind through the band or rim joist of a floor to the construction below. If additional cross-grain tension strength is required, the inspector should increase member size or consider alternative construction details that reduce cross-grain tension forces. When excessive tension stress perpendicular to grain cannot be avoided, the use of mechanical reinforcement or design detailing to reduce the cross-grain tension forces is considered good practice (particularly in high-hazard seismic regions) to ensure that brittle failures do not occur.
Structural Serviceability
Deflection Due to Bending
The NDS does not specifically limit deflection but rather defers to inspector judgment or building code specifications. Nonetheless, with many interior and exterior finishes susceptible to damage by large deflections, reasonable deflection limits based on design loads are recommended herein for the design of specific elements.
The calculation of member deflection is based on the section properties of the beam from NDS-S and the member’s modulus of elasticity with applicable adjustments. Generally, a deflection check using the equations below is based on the estimated maximum deflection under a specified loading condition. Given that wood exhibits time- and load-magnitude-dependent permanent deflection (creep), the total long-term deflection can be estimated in terms of two components of the load related to short- and long-term deflection using recommendations provided in NDS 3.5.

If a deflection check proves unacceptable, the inspector may increase member depth, decrease the clear span or spacing of the member, or select a grade and species of wood with a higher modulus of elasticity (the least effective option). Typical denominator values used in the deflection equation range from 120 to 600, depending on application and inspector judgment. Table 5.5 provides recommended deflection limits. Certainly, if a modest adjustment to a deflection limit results in a more efficient design, the inspector should exercise discretion with respect to a possible negative consequence, such as vibration or long-term creep. For lateral bending loads on walls, a serviceability load for a deflection check may be considered as a fraction of the nominal design wind load for exterior walls. A reasonable serviceability wind load criteria may be taken as 0.75W or 75% of the nominal design wind load.
TABLE 5.5 Recommended Allowable Deflection Limits

Given that system effects influence the stiffness of assemblies in a manner similar to that of bending capacity (see Section 5.2.4.2), the system deflection factors of Table 5.6 are recommended. The estimated deflection based on an analysis of an element (e.g., stud or joist) is multiplied by the deflection factors to account for system effect. Typical deflection checks on floors under uniform loading can be easily overestimated by 20% or more. In areas where partitions add to the rigidity of the supporting floor, deflection can be overestimated by more than 50% (Hurst, 1965). When concentrated loads are considered on typical light-frame floors with wood structural panel subflooring, deflections can be overestimated by a factor of 2.5 to 3 due to the neglect of the load distribution to adjacent framing members and partial composite action (Tucker and Fridley, 1999). Similar results have been found for sheathed wall assemblies (NAHBRF, 1974). When adhesives attach wood structural panels to wood framing, even greater reductions in deflection are realized due to increased composite action (Gillespie et al., 1978; Pellicane and Anthony, 1996). However, if a simple deflection limit, such as /360, is construed to control floor vibration in addition to the serviceability of finishes, the use of system deflection factors of Table 5.6 is not recommended for floor system design. In this case, a more accurate estimate of actual deflection may result in a floor with increased tendency to vibrate or bounce.
TABLE 5.6 System Deflection Adjustment Factors

Floor Vibration

The NDS does not specifically address floor vibration because it is a serviceability rather than a safety issue. In addition, what is considered an acceptable amount of floor vibration is highly subjective. Accordingly, reliable design information on controlling floor vibration to meet a specific level of acceptance is not readily available; therefore, some rules of thumb are provided below for the inspector wishing to limit vibration beyond that implied by the traditional use of an /360 deflection limit (FHA, 1958; Woeste and Dolan, 1998).
- For floor joist spans less than 15 feet, a deflection limit of /360 considering design live loads only may be used, where is the clear span of the joist in inches.
- For floor joist clear spans greater than 15 feet, the maximum deflection should be limited to 0.5 inches.
- For wood I-joists, the manufacturer’s tables that limit deflection to /480 should be used for spans greater than 15 feet, where is the clear span of the member in inches.
- When calculating deflection based on the above rules of thumb, the inspector should use a 40 psf live load for all rooms, whether or not they are considered sleeping rooms.
- As an additional recommendation, glue and mechanically fasten the floor sheathing to the floor joists to enhance the floor system’s strength and stiffness.
Floor deflections are typically limited to /360 in the span tables published in current building codes using a standard deflection check without consideration of system effects. For clear spans greater than 15 feet, this deflection limit has caused nuisance vibrations that are unacceptable to some building occupants or owners. Floor vibration is also aggravated when the floor is supported on a bending member (e.g., girder) rather than on a rigid bearing wall. It may be desirable to design such girders with a smaller deflection limit to control floor vibration, particularly when girder and floor spans have more than a 20-foot total combined span (i.e., span of girder plus span of supported floor joist).
For metal plate-connected wood trusses, strong-backs are effective in reducing floor vibration when they are installed through the trusses near the center of the span. A strong-back is a continuous bracing member, typically a 2x6, fastened edgewise to the base of the vertical web of each truss with two 16d nails. For longer spans, strong-backs may be spaced at approximately 8-foot intervals across the span. Details for strong-backs may be found in the Metal Plate-Connected Wood Truss Handbook (WTCA, 1997). Alternatively, a more stringent deflection criteria may be used for the floor truss design.
Shrinkage
The amount of wood shrinkage in a structure depends on the moisture content (MC) of the lumber at the time of installation relative to the equilibrium moisture content (EMC) that the wood will ultimately attain in use. It is also dependent on the detailing of the structure, such as the amount of lumber supporting loads in a perpendicular-to-grain orientation (i.e., sill, sole, top plates and joists). MC at installation is a function of the specified drying method, jobsite storage practices, and climate conditions during construction. Relatively dry lumber (15% or less) minimizes shrinkage problems affecting finish materials and prevents loosening or stressing of connections. A less favorable but acceptable alternative is to detail the structure such that shrinkage is uniform, dispersed, or otherwise designed to minimize problems. This alternative is the defacto choice in simple residential buildings.
Shrinking and swelling across the width or thickness of lumber can be estimated by the equation below from ASTM D1990 for typical softwood structural lumber (ASTM, 1998a). Shrinkage in the longitudinal direction of the member is practically negligible.

Floor Framing
The objectives of floor system design are:
- to support occupancy live loads and building dead loads adequately;
- to resist lateral forces resulting from wind and seismic loads and to transmit the forces to supporting shear walls through diaphragm action;
- to provide a suitable subsurface for floor finishes;
- to avoid owner complaints (e.g., excessive vibration, noise, etc.);
- to serve as a thermal barrier over unconditioned areas (e.g., crawl spaces); and
- to provide a one- to two-hour fire rating between dwelling units in multi-family buildings (refer to local building codes).
General
A wood floor is a horizontal structural system composed primarily of the following members:
◦ joists;
◦ girders; and
◦ sheathing.
Wood floor systems have traditionally been built of solid-sawn lumber for floor joists and girders, although parallel chord wood trusses and wood I-joists are seeing increasing use, and offer advantages for dimensional consistency, and spans. Floor joists are horizontal, repetitive framing members that support the floor sheathing and transfer the live and dead floor loads to the walls, girders, or columns below. Girders are horizontal members that support floor joists not otherwise supported by interior or exterior load-bearing walls. Floor sheathing is a horizontal structural element, usually plywood or oriented strand board panels, that directly supports floor loads and distributes the loads to the framing system below. Floor sheathing also provides lateral support to the floor joists. As a structural system, the floor provides resistance to lateral building loads resulting from wind and seismic forces and thus constitutes a horizontal diaphragm. Refer to Figure 5.2 for an illustration of floor system structural elements and to Cost-Effective Home Building: A Design and Construction Handbook for efficient design ideas and concepts.
FIGURE 5.2 Structural Elements of the Floor System

The design approach discussed herein addresses solid-sawn lumber floor systems in accordance with the procedures specified in the National Design Specification for Wood Construction (NDS), with appropriate modifications as noted. For more information regarding wood I-joists, trusses, and other materials, consult the manufacturer’s specifications and applicable code evaluation reports.
When inspecting any structural element, the inspector must first determine the loads acting on the element. Given that only the dead loads of the floor system and live loads of occupancy are present in a typical floor system, the controlling design load combination for a simply-supported floor joist is D+L.
For joists with more complicated loading, such as cantilevered joists supporting roof framing, the following load combinations may be considered:
Readily available tables in residential building codes provide maximum allowable spans for different species, grades, sizes, and spacings of lumber joists. Some efficient concepts for floor joist design are also provided in Cost-Effective Home Building: A Design and Construction Handbook (NAHB). Therefore, it is usually not necessary to design conventional floor joists for residential construction. To obtain greater economy or performance, however, inspectors may wish to create their own span tables or spreadsheets for future use in accordance with the methods shown in this section.
Keep in mind that the grade and species of lumber is often a regional choice governed by economics and availability; some of the most common species of lumber for floor joists are hem-fir, spruce-pine-fir, Douglas fir, and southern yellow pine. Bear in mind, too, that the most common sizes for floor joists are 2x8 and 2x10, although 2x12s are also frequently used.
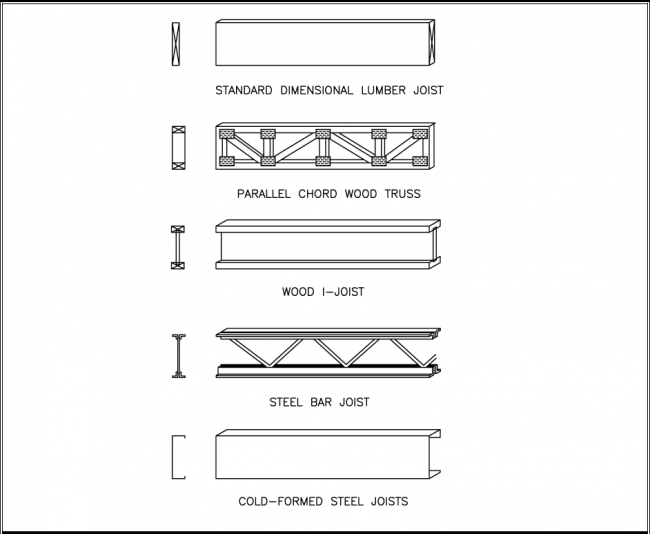
For different joist applications, such as a continuous multiple span, the inspector should use the appropriate beam equations to estimate the stresses induced by the loads and reactions. Other materials, such as wood I-joists and parallel chord floor trusses, are also commonly used in light-frame residential and commercial construction; refer to the manufacturer’s data for span tables for wood I-joists and other engineered wood products. Cold-formed steel floor joists or trusses may also be considered. Figure 5.3 illustrates some conventional and alternative floor joist members.
D + LFloor Joist Design
D + L + 0.3 (Lr or S)
D + (Lr or S) + 0.3L
Readily available tables in residential building codes provide maximum allowable spans for different species, grades, sizes, and spacings of lumber joists. Some efficient concepts for floor joist design are also provided in Cost-Effective Home Building: A Design and Construction Handbook (NAHB). Therefore, it is usually not necessary to design conventional floor joists for residential construction. To obtain greater economy or performance, however, inspectors may wish to create their own span tables or spreadsheets for future use in accordance with the methods shown in this section.
Keep in mind that the grade and species of lumber is often a regional choice governed by economics and availability; some of the most common species of lumber for floor joists are hem-fir, spruce-pine-fir, Douglas fir, and southern yellow pine. Bear in mind, too, that the most common sizes for floor joists are 2x8 and 2x10, although 2x12s are also frequently used.
For different joist applications, such as a continuous multiple span, the inspector should use the appropriate beam equations to estimate the stresses induced by the loads and reactions. Other materials, such as wood I-joists and parallel chord floor trusses, are also commonly used in light-frame residential and commercial construction; refer to the manufacturer’s data for span tables for wood I-joists and other engineered wood products. Cold-formed steel floor joists or trusses may also be considered. Figure 5.3 illustrates some conventional and alternative floor joist members.
FIGURE 5.3 Conventional and Alternative Floor Framing Members
For typical floor systems supporting a concentrated load at or near center span, load distribution to adjacent joists can substantially reduce the bending stresses or moment experienced by the loaded joist. A currently available design methodology may be beneficial for certain applications, such as wood-framed garage floors that support heavy concentrated wheel loads. Under such conditions, the maximum bending moment experienced by any single joist is reduced by more than 60%. A similar reduction in the shear loading (and end reaction) of the loaded joist also results, with exceptions for moving concentrated loads that may be located near the end of the joist, thus creating a large transverse shear load with a small bending moment. The above-mentioned design methodology for a single, concentrated load applied near mid-span of a repetitive member floor system is essentially equivalent to using a Cr factor of 1.5 or more. The system deflection adjustment factors in Table 5.6 are applicable as indicated for concentrated loads.
Bridging or cross-braces were formerly thought to provide both necessary lateral-torsional bracing of dimensional lumber floor joists and stiffer floor systems. However, full-scale testing of 10 different floor systems as well as additional testing in completed homes has conclusively demonstrated that bridging or cross-bracing provides negligible benefit to either the load-carrying capacity or stiffness of typical residential floors with dimensional lumber framing (sizes of 2x6 through 2x12) and wood structural panel subflooring (NAHB, 1961). These same findings are not proven to apply to other types of floor joists (i.e., I-joists, steel joists, etc.) or for dimensional lumber joists greater than 12 inches in depth. According to the study, bridging may be considered necessary for 2x10 and 2x12 dimensional lumber joists with clear spans exceeding about 16 feet and 18 feet, respectively (based on a 50 psf total design load and L/360 deflection limit). To the contrary, the beam stability provisions of NDS 4.4.1 conservatively require bridging to be spaced at intervals not exceeding 8 feet along the span of 2x10 and 2x12 joists.
Girder Design
The decision to use one girder over another is a function of cost, availability, span and loading conditions, clearance or head-room requirements, and ease of construction. Refer to the Figure 5.4 for illustrations of girder types.

For typical floor systems supporting a concentrated load at or near center span, load distribution to adjacent joists can substantially reduce the bending stresses or moment experienced by the loaded joist. A currently available design methodology may be beneficial for certain applications, such as wood-framed garage floors that support heavy concentrated wheel loads. Under such conditions, the maximum bending moment experienced by any single joist is reduced by more than 60%. A similar reduction in the shear loading (and end reaction) of the loaded joist also results, with exceptions for moving concentrated loads that may be located near the end of the joist, thus creating a large transverse shear load with a small bending moment. The above-mentioned design methodology for a single, concentrated load applied near mid-span of a repetitive member floor system is essentially equivalent to using a Cr factor of 1.5 or more. The system deflection adjustment factors in Table 5.6 are applicable as indicated for concentrated loads.
Bridging or cross-braces were formerly thought to provide both necessary lateral-torsional bracing of dimensional lumber floor joists and stiffer floor systems. However, full-scale testing of 10 different floor systems as well as additional testing in completed homes has conclusively demonstrated that bridging or cross-bracing provides negligible benefit to either the load-carrying capacity or stiffness of typical residential floors with dimensional lumber framing (sizes of 2x6 through 2x12) and wood structural panel subflooring (NAHB, 1961). These same findings are not proven to apply to other types of floor joists (i.e., I-joists, steel joists, etc.) or for dimensional lumber joists greater than 12 inches in depth. According to the study, bridging may be considered necessary for 2x10 and 2x12 dimensional lumber joists with clear spans exceeding about 16 feet and 18 feet, respectively (based on a 50 psf total design load and L/360 deflection limit). To the contrary, the beam stability provisions of NDS 4.4.1 conservatively require bridging to be spaced at intervals not exceeding 8 feet along the span of 2x10 and 2x12 joists.
Girder Design
The decision to use one girder over another is a function of cost, availability, span and loading conditions, clearance or head-room requirements, and ease of construction. Refer to the Figure 5.4 for illustrations of girder types.
Girders in residential construction are usually one of the following types:
◦ built-up dimensional lumber;
◦ steel I-beam;
◦ engineered wood beam;
◦ site-fabricated beam;
◦ wood I-joist; or
◦ metal plate connected wood truss.
Built-up beams are constructed by nailing together of two or more plys of dimensional lumber. Since load sharing occurs between the plys (i.e., lumber members), the built-up girder is able to resist higher loads than a single member of the same overall dimensions. The built-up member can resist higher loads only if butt joints are located at or near supports and are staggered in alternate plys. Each ply may be face nailed to the previous ply with 10d nails staggered at 12 inches on center top to bottom. The design method and equations are the same as those in Section 5.4.2 for floor joists; however, the adjustment factors applying to design values and loading conditions are somewhat different.
◦ built-up dimensional lumber;
◦ steel I-beam;
◦ engineered wood beam;
◦ site-fabricated beam;
◦ wood I-joist; or
◦ metal plate connected wood truss.
Built-up beams are constructed by nailing together of two or more plys of dimensional lumber. Since load sharing occurs between the plys (i.e., lumber members), the built-up girder is able to resist higher loads than a single member of the same overall dimensions. The built-up member can resist higher loads only if butt joints are located at or near supports and are staggered in alternate plys. Each ply may be face nailed to the previous ply with 10d nails staggered at 12 inches on center top to bottom. The design method and equations are the same as those in Section 5.4.2 for floor joists; however, the adjustment factors applying to design values and loading conditions are somewhat different.
The inspector needs to keep the following in mind:
- Although floor girders are not typically thought of as repetitive members, a repetitive-member factor is applicable if the floor girder is built up from two or more members (three or more, according to the NDS).
- The beam stability factor, CL, is determined in accordance with NDS•3.3.3; however, for girders supporting floor framing, lateral support is considered to be continuous and CL = 1.
FIGURE 5.4 Examples of Beams and Girders

Steel I-beams are often used in residential construction because of their greater spanning capability. Compared with wood members, they span longer distances with a shallower depth. A 2x4 or 2x6 is usually attached to the top surface with bolts to provide a fastening surface for floor joists and other structural members. Although steel beam shapes are commonly referred to as I-beams, a typical 8-inch-deep W-shaped beam is commonly considered a house beam. Alternatively, built-up cold-formed steel beams (i.e., back-to-back C-shapes) may be used to construct I-shaped girders.
Engineered wood beams include I-joists, wood trusses (i.e., girder trusses) glue-laminated lumber, laminated veneer lumber, parallel strand lumber, etc. This guide does not address the design of engineered wood girders because product manufacturers typically provide span tables or engineered designs that are considered proprietary. Consult the manufacturer for design guidelines or completed span tables.
Site-fabricated beams include plywood box beams, plywood I-beams, and flitch plate beams. Plywood box beams are fabricated from continuous dimensional lumber flanges (typically 2x4s or 2x6s) sandwiched between two plywood webs; stiffeners are placed at concentrated loads, end-bearing points, plywood joints, and maximum 24-inch intervals. Plywood I-beams are similar to box beams except that the plywood web is sandwiched between dimensional lumber wood flanges (typically 2x4s or 2x6s), and stiffeners are placed at maximum 24-inch intervals. Flitch plate beams are fabricated from a steel plate sandwiched between two pieces of dimensional lumber to form a composite section. Thus, a thinner member is possible in comparison to a built-up wood girder of similar strength. The steel plate is typically 1/4- to 1/2-inch-thick and about 1/4-inch less in depth than the dimensional lumber. The sandwich construction is usually assembled with through-bolts staggered at about 12 inches on center. Flitch plate beams derive their strength and stiffness from the composite section of steel plate and dimensional lumber. The lumber also provides a medium for fastening other materials using nails or screws.
Span tables for plywood I-beams, plywood box beams, steel-wood I-beams, and flitch plate beams are provided in NAHB's Beam Series publications. The International One- and Two-Family Dwelling Code (ICC) provides a simple prescriptive table for plywood box beam headers.
Subfloor Design
Typical subfloor sheathing is nominal 5/8- or 3/4-inch-thick 4x8 panels of plywood or oriented strand board (OSB) with tongue-and-groove edges at unsupported joints perpendicular to the floor framing. Sheathing products are generally categorized as wood structural panels and are specified in accordance with the prescriptive span rating tables published in a building code or are made available by the manufacturer. The prescriptive tables provide maximum spans (joist spacing) based on sheathing thickness and span rating. It is important to note that the basis for the prescriptive tables is the standard beam calculation. If loads exceed the limits of the prescriptive tables, the inspector may be required to perform calculations; however, such calculations are rarely necessary. In addition, the APA offers a plywood floor guide for residential garages that assist in specifying plywood subflooring suitable for heavy concentrated loads from vehicle tire loading.
The APA also recommends a fastener schedule for connecting sheathing to floor joists. Generally, nails are placed a minimum of 6 inches on center at edges and 12 inches on center along intermediate supports. Nail sizes vary with nail type (e.g., sinkers, box nails, and common nails), and various nail types have different characteristics that affect structural properties. For information on other types of fasteners, consult the manufacturer. In some cases, shear loads in the floor diaphragm resulting from lateral loads (i.e., wind and earthquake) may require a more stringent fastening schedule. Regardless of fastener type, gluing the floor sheathing to the joists increases floor stiffness and strength.
TABLE 5.7 Fastening Floor Sheathing to Structural Members

While not as common today, boards may also be used as a subfloor (i.e., board sheathing). Floor sheathing boards are typically 1x6 or 1x8 material laid flatwise and diagonally (or perpendicular) on the floor joists. They may be designed using the NDS or local accepted practice.
Wall Framing
The objectives of wall system design are:
- to resist snow, live and dead loads, and wind and seismic forces;
- to provide an adequate subsurface for wall finishes, and to provide openings for doors and windows;
- to serve as a thermal and weather barrier;
- to provide space and access for electrical and mechanical equipment, where required; and
- to provide a one- to two-hour fire barrier if the wall separates individual dwelling units in attached or multi-family buildings.
General

A wall is a vertical structural system that supports gravity loads from the roof and floors above and transfers the loads to the foundation below. It also resists lateral loads resulting from wind and earthquakes.
A typical wood-framed wall is composed of the following elements as shown in Figure 5.5:
◦ studs, including wall, cripple, jack, and king studs;
◦ top and bottom (sole) plates;
◦ headers;
◦ sheathing; and
◦ diagonal let-in braces, if used.
Residential wall systems have traditionally been constructed of dimensional lumber, usually 2x4s or 2x6s, although engineered wood studs and cold-formed steel studs are now seeing increased use. Wall studs are vertical, repetitive framing members spaced at regular intervals to support the wall sheathing. They span the full height of each story and support the building loads above. King and jack studs (also known as jamb studs) frame openings and support loads from a header. Cripple studs are placed above or below a wall opening and are not full-height. Built-up wall studs that are assembled on the jobsite may be used within the wall to support concentrated loads. Top and bottom plates are horizontal members to which studs are fastened. The top and bottom plates are then fastened to the floor or roof above and either to the floor below or directly to the foundation. Headers are beams that transfer the loads above an opening to jack studs at each side of the opening.
FIGURE 5.5 Structural Elements of the Wall System
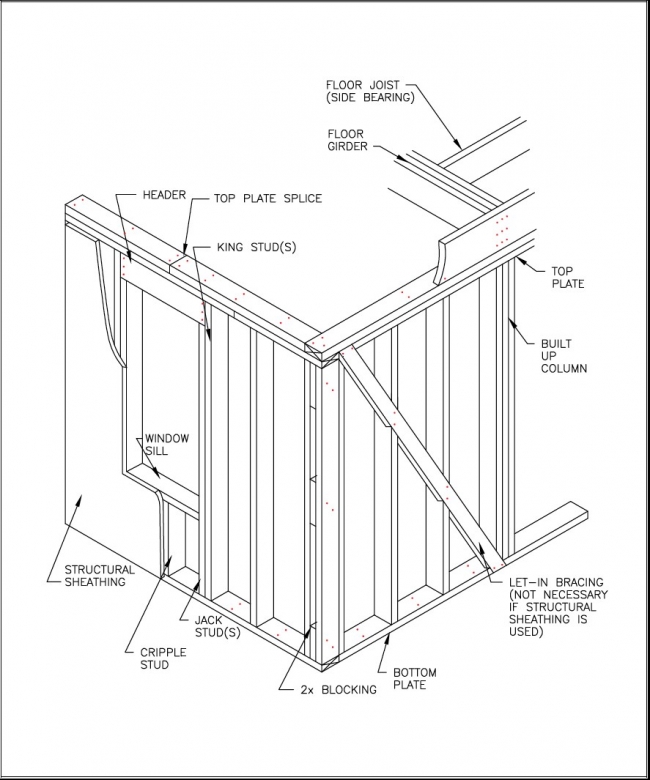
Structural wall sheathing, such as plywood or oriented strand board, distributes lateral loads to the wall framing and provides lateral support to both the wall studs (i.e., buckling resistance) and the entire building (i.e., racking resistance). Interior wall finishes also provide significant support to the wall studs and the structure. In low-wind and low-hazard seismic areas, metal T-braces or wood let-in braces may be used in place of wall sheathing to provide resistance to lateral (i.e., racking) loads. About 50% of new homes constructed each year now use wood structural panel braces, and many of those homes are fully sheathed with wood structural panels. These bracing methods are substantially stronger than the let-in brace approach. Wood let-in braces are typically 1x4 wood members that are "let in" or notched into the studs and nailed diagonally across wall sections at corners and specified intervals. Their use is generally through application of conventional construction provisions found in most building codes for residential construction in combination with interior and exterior claddings.
The design procedure discussed herein addresses dimensional lumber wall systems according to the National Design Specification for Wood Construction (NDS). Where appropriate, modifications to the NDS have been incorporated and are noted. Standard design equations and design checks for the NDS procedure were presented earlier.
Wall systems are designed to withstand dead and live gravity loads acting parallel to the wall stud length, as well as lateral loads–primarily wind and earthquake loads–acting perpendicular to the face of the wall. Wind also induces uplift loads on the roof; when the wind load is sufficient to offset dead loads, walls and internal connections must be designed to resist tension or uplift forces. The outcome of the design of wall elements depends on the degree to which the inspector uses the system strength inherent in the construction.
◦ studs, including wall, cripple, jack, and king studs;
◦ top and bottom (sole) plates;
◦ headers;
◦ sheathing; and
◦ diagonal let-in braces, if used.
Residential wall systems have traditionally been constructed of dimensional lumber, usually 2x4s or 2x6s, although engineered wood studs and cold-formed steel studs are now seeing increased use. Wall studs are vertical, repetitive framing members spaced at regular intervals to support the wall sheathing. They span the full height of each story and support the building loads above. King and jack studs (also known as jamb studs) frame openings and support loads from a header. Cripple studs are placed above or below a wall opening and are not full-height. Built-up wall studs that are assembled on the jobsite may be used within the wall to support concentrated loads. Top and bottom plates are horizontal members to which studs are fastened. The top and bottom plates are then fastened to the floor or roof above and either to the floor below or directly to the foundation. Headers are beams that transfer the loads above an opening to jack studs at each side of the opening.
FIGURE 5.5 Structural Elements of the Wall System

Structural wall sheathing, such as plywood or oriented strand board, distributes lateral loads to the wall framing and provides lateral support to both the wall studs (i.e., buckling resistance) and the entire building (i.e., racking resistance). Interior wall finishes also provide significant support to the wall studs and the structure. In low-wind and low-hazard seismic areas, metal T-braces or wood let-in braces may be used in place of wall sheathing to provide resistance to lateral (i.e., racking) loads. About 50% of new homes constructed each year now use wood structural panel braces, and many of those homes are fully sheathed with wood structural panels. These bracing methods are substantially stronger than the let-in brace approach. Wood let-in braces are typically 1x4 wood members that are "let in" or notched into the studs and nailed diagonally across wall sections at corners and specified intervals. Their use is generally through application of conventional construction provisions found in most building codes for residential construction in combination with interior and exterior claddings.
The design procedure discussed herein addresses dimensional lumber wall systems according to the National Design Specification for Wood Construction (NDS). Where appropriate, modifications to the NDS have been incorporated and are noted. Standard design equations and design checks for the NDS procedure were presented earlier.
Wall systems are designed to withstand dead and live gravity loads acting parallel to the wall stud length, as well as lateral loads–primarily wind and earthquake loads–acting perpendicular to the face of the wall. Wind also induces uplift loads on the roof; when the wind load is sufficient to offset dead loads, walls and internal connections must be designed to resist tension or uplift forces. The outcome of the design of wall elements depends on the degree to which the inspector uses the system strength inherent in the construction.
When inspecting wall elements, the inspector needs to consider the load combinations, particularly the following ASD combinations of dead, live, snow and wind loads:
◦ D + L + 0.3 (Lr or S)
◦ D + (Lr or S) + 0.3 L
◦ D + W
◦ D + 0.7E + 0.5L + 0.2S
A wall system may support a roof only or a roof and one or more stories above. The roof may or may not include an attic storage live load. A 10 psf attic live load used for the design of ceiling joists is intended primarily to provide safe access to the attic, not storage. The controlling load combination for a wall that supports only a roof is the second load combination listed above. If the attic is not intended for storage, the value for L should be 0. The controlling load combination for a wall that supports a floor, wall and a roof should be either the first or second load combination, depending on the relative magnitude of floor and roof snow loads.
The third load combination provides a check for the out-of-plane bending condition due to lateral wind loads on the wall. For tall wood-frame walls that support heavy claddings, such as brick veneer, the inspector should also consider out-of-plane bending loads resulting from an earthquake load combination, although the other load combinations above usually control the design. The third and fourth load combinations are essentially combined bending and axial loads that may govern stud design as opposed to axial load only in the first two load combinations.
In many cases, certain design load combinations or load components can be dismissed or eliminated through practical consideration and inspection. They are a matter of inspector judgment, experience, and knowledge of the critical design conditions.
Load-Bearing Walls
Exterior load-bearing walls support both axial and lateral loads. For interior load-bearing walls, only gravity loads are considered. A serviceability check using a lateral load of 5 psf is sometimes applied independently to interior walls but should not normally control the design of load-bearing framing. This section focuses on the axial and lateral load-bearing capacity of exterior and interior walls.
◦ D + L + 0.3 (Lr or S)
◦ D + (Lr or S) + 0.3 L
◦ D + W
◦ D + 0.7E + 0.5L + 0.2S
A wall system may support a roof only or a roof and one or more stories above. The roof may or may not include an attic storage live load. A 10 psf attic live load used for the design of ceiling joists is intended primarily to provide safe access to the attic, not storage. The controlling load combination for a wall that supports only a roof is the second load combination listed above. If the attic is not intended for storage, the value for L should be 0. The controlling load combination for a wall that supports a floor, wall and a roof should be either the first or second load combination, depending on the relative magnitude of floor and roof snow loads.
The third load combination provides a check for the out-of-plane bending condition due to lateral wind loads on the wall. For tall wood-frame walls that support heavy claddings, such as brick veneer, the inspector should also consider out-of-plane bending loads resulting from an earthquake load combination, although the other load combinations above usually control the design. The third and fourth load combinations are essentially combined bending and axial loads that may govern stud design as opposed to axial load only in the first two load combinations.
In many cases, certain design load combinations or load components can be dismissed or eliminated through practical consideration and inspection. They are a matter of inspector judgment, experience, and knowledge of the critical design conditions.
Load-Bearing Walls
Exterior load-bearing walls support both axial and lateral loads. For interior load-bearing walls, only gravity loads are considered. A serviceability check using a lateral load of 5 psf is sometimes applied independently to interior walls but should not normally control the design of load-bearing framing. This section focuses on the axial and lateral load-bearing capacity of exterior and interior walls.

Exterior walls are not necessarily load-bearing walls. Load-bearing walls support gravity loads from either the roof, ceiling, or floor joists or the beams above. A gable-end wall is typically considered to be a non-load-bearing wall in that roof and floor framing generally runs parallel to the gable end; however, it must support lateral wind and seismic loads and even small dead and live loads. Exterior load-bearing walls must be designed for axial loads as well as for lateral loads from wind or seismic forces. They must also act as shear walls to resist racking loads from lateral wind or seismic forces on the overall building.
When calculating the column stability factor for a stud wall, note that column capacity is determined by using the slenderness ratio about the strong axis of the stud (le/d)x. The reason for using the strong axis slenderness ratio is that lateral support is provided to the stud by the wall sheathing and finish materials in the stud’s weak-axis bending or buckling direction. When determining the column stability factor, CP, for a wall system rather than for a single column in accordance with NDS 3.7.1, the inspector must exercise judgment with respect to the calculation of the effective length, e, and the depth or thickness of the wall system, d. A buckling coefficient, Ke, of about 0.8 is reasonable (see Appendix G of NDS) and is supported in the research literature on this topic for sheathed wall assemblies and studs with square-cut ends (i.e., not a pinned joint).
In cases where continuous support is not present (e.g., during construction), the inspector may want to consider stability for both axes. Unsupported studs generally fail due to weak-axis buckling under a significantly lower load than would otherwise be possible with continuous lateral support in the weak-axis buckling direction.
Interior walls may be either load-bearing or non-load-bearing. Non-load-bearing interior walls are often called partitions (see Section 5.5.3). In either case, interior walls should be solidly fastened to the floor and ceiling framing and to the exterior wall framing where they abut. It may be necessary to install extra studs, blocking, or nailers in the outside walls to provide for attachment of interior walls. The framing must also be arranged to provide a nailing surface for wall-covering materials at inside corners. For efficient construction details and concepts related to wall framing, refer to Cost-Effective Home Building: A Design and Construction Handbook.
Interior load-bearing walls typically support the floor or ceiling joists above when the clear span from exterior wall to exterior wall is greater than the spanning capability of the floor or ceiling joists. Interior walls, unlike exterior walls, seldom experience large transverse or out-of-plane lateral loads; however, some building codes require interior walls to be designed for a minimum lateral load, such as 5 psf, for serviceability. Generally, axial load design provides more than adequate resistance to a nominal lateral load.
If local code requirements do require wall studs to be designed to withstand a minimum lateral load, the inspector should recommend load-bearing walls in accordance with the previous section on exterior load bearing walls.
Non-Load-Bearing Partitions
Interior partitions are not intended to support structural loads. Standard 2x4 or 2x3 wood stud interior partition walls are well proven in practice and do not require analysis. Openings within partitions do not require headers or trimmers and are commonly framed with single studs and horizontal members of the same size as the studs. Particularly in the case of closets or other tight spaces, builders may frame certain partitions with smaller lumber, such as 2x2 studs or 2x4 studs turned flatwise to save space.
Where a minimum 5 psf lateral load check for serviceability is required in a non-load-bearing partition, the stud may be designed as a bending member or system similar to a simply supported floor joist, except that the only load is a 5 psf load uniformly distributed. The design approach and system factors in Sections 5.2 and 5.3 apply as appropriate.
Headers
Load-bearing headers are horizontal members that carry loads from a wall, ceiling, floor or roof above and transfer the combined load to jack and king studs on each side of a window or door opening. The span of the header may be taken as the width of the rough opening measured between the jack studs supporting the ends of the header. Headers are usually built up from two nominal 2-inch-thick members.

Load-bearing header design and fabrication is similar to that for girders. This guide considers headers consisting of double members to be repetitive members; therefore, a repetitive member factor, Cr, of 1.1 to 1.2 should apply, along with a live load deflection limit of /240. Large openings or especially heavy loads may require stronger members, such as engineered wood beams, hot-rolled steel, or flitch plate beams.
Headers are generally designed to support all loads from above; however, typical residential construction calls for a double top plate above the header. When an upper story is supported, a floor band joist and sole plate of the wall above are also spanning the wall opening below. These elements are all part of the resisting system. Recent testing determined whether an adjustment factor (i.e., system factor or repetitive member factor) is justified in designing a header. The results showed that a repetitive member factor is valid for headers constructed of only two members, as shown in Table 5.4, and that additional system effects produce large increases in capacity when the header is overlaid by a double top plate, band joist and sole plate. Consequently, an overall system factor of 1.8 was found to be a simple, conservative design solution. That system factor is applicable to the adjusted bending stress value, Fb, of the header member only. While this example covers only a very specific condition, it exemplifies the magnitude of potential system effect in similar conditions. In this case, the system effect is associated with load sharing and partial composite action. The above adjustment factor is not currently recognized in the NDS.
TABLE 5.8 Recommended System Adjustment Factors for Header Design

Headers are not required in non-load-bearing walls. Openings can be framed with single studs and a horizontal header block of the same size. It is common practice to use a double 2x4 or triple 2x4 header for larger openings in non-load-bearing walls. In the interest of added rigidity and fastening surface, however, some builders use additional jamb studs for openings in non-load-bearing walls, but such studs are not required.
Columns
Columns are vertical members placed where an axial force is applied parallel to the longitudinal axis. Columns may fail by either crushing or buckling. Longer columns have a higher tendency than shorter columns to fail due to buckling. The load at which the column buckles (Euler buckling load) is directly related to the ratio of the column’s unsupported length to its depth (slenderness factor).
Figure 5.6 illustrates three ways to construct columns using lumber. Simple columns are columns fabricated from a single piece of sawn lumber; spaced columns are fabricated from two or more individual members with their longitudinal axes parallel and separated with blocking at their ends and midpoint(s); and built-up columns are solid columns fabricated from several individual members fastened together. Spaced columns as described in the NDS are not normally used in residential buildings and are not addressed here.
Steel jack posts are also commonly used in residential construction; however, jack post manufacturers typically provide a rated capacity so that no design is required except the specification of the design load requirements and the selection of a suitable jack post that meets or exceeds the required loading. Typical 8-foot-tall steel jack posts are made of pipe and have adjustable bases for floor leveling. The rated (design) capacity generally ranges from 10,000 to 20,000 pounds, depending on the steel pipe's diameter and wall thickness.
Simple columns are fabricated from one piece of sawn lumber. In residential construction, simple columns, such as a 4x4, are common.
Built-up columns are fabricated from several wood members fastened together with nails or bolts. They are commonly used in residential construction because smaller members can be easily fastened together at the jobsite to form a larger column with adequate capacity.
The nails or bolts used to connect the plys (i.e., the separate members) of a built-up column do not rigidly transfer shear loads; therefore, the bending load capacity of a built-up column is less than a single column of the same species, grade, and cross-sectional area when bending direction is perpendicular to the laminations (i.e., all members bending in their individual weak-axis direction). The coefficient Kf accounts for the capacity reduction in bending load in nailed or bolted built-up columns. It applies, however, only to the weak-axis buckling or bending direction of the individual members and therefore should not be used to determine CP for column buckling in the strong-axis direction of the individual members.
The above consideration is not an issue when the built-up column is sufficiently braced in the weak-axis direction (i.e., embedded in a sheathed wall assembly). In this typical condition, the built-up column is actually stronger than a solid-sawn member of equivalent size and grade because of the repetitive member effect on bending capacity. However, when the members in the built-up column are staggered or spliced, the column bending strength is reduced. While the NDS 15.3 provisions apply only to built-up columns with all members extending the full height of the column, design methods for spliced columns are available.
FIGURE 5.6 Wood Column Types

Roofs
The objectives of roof framing design are:
- to support building dead and snow loads and to resist wind and seismic forces;
- to resist roof construction and maintenance loads;
- to provide a thermal and weather barrier;
- to provide support for interior ceiling finishes; and
- to provide attic space and access for electrical and mechanical equipment or storage.
General
A roof in residential construction is typically a sloped structural system that supports gravity and lateral loads and transfers the loads to the walls below.
Generally, the four options for wood roof construction are:
- roof trusses;
- rafters and cross-ties;
- rafters with ridge beams (i.e. cathedral ceiling); and
- timber framing.

By far the most common types of residential roof construction use light-frame trusses, rafters, or a mix of these, depending on roof layout. Rafters are repetitive framing members that support the roof sheathing and typically span from the exterior walls to a non-structural ridge board (i.e., reaction plate). Rafter pairs may also be joined at the ridge with a gusset, thereby eliminating the need for a ridge board. Rafters may also be braced at or near mid-span using intermittent 2x vertical braces and a 2x runner crossing the bottom edges of the rafters. Ceiling joists are repetitive framing members that support ceiling and attic loads and transfer the loads to the walls and beams below. They are not normally designed to span between exterior walls and therefore require an intermediate bearing wall. Overhangs, where used, are framed extensions of the roof that extend beyond the exterior wall of the home, typically by 1 to 2 feet. Overhangs protect walls and windows from direct sun and rain and therefore offer durability and energy efficiency benefits.
Ceiling joists are typically connected to rafter pairs to resist outward thrust generated by loading on the roof. Where ceiling joists or cross-ties are eliminated to create a cathedral ceiling, a structural ridge beam must be used to support the roof at the ridge and to prevent outward thrust of the bearing walls. Ceiling joists and roof rafters are bending members that are designed similarly; therefore, this article groups them under one section.
FIGURE 5.7 Structural Elements of a Conventional Roof System

Roof trusses are pre-engineered components. They are fabricated from 2-inch-thick dimensional lumber connected with metal truss plates. They are generally more efficient than stick framing and are usually designed to span from exterior wall to exterior wall with no intermediate support. In more complex portions of roof systems, it is still common to use rafter framing techniques.
Roof sheathing is a thin structural element, usually plywood or oriented strand board, that supports roof loads and distributes lateral and axial loads to the roof framing system. Roof sheathing also provides lateral support to the roof framing members and serves as a membrane or diaphragm to resist and distribute lateral building loads from wind or earthquakes.
Roof systems are designed to withstand dead, live, snow and wind uplift loads; in addition, they are designed to withstand lateral loads, such as wind and earthquake loads, transverse to the roof system. The design procedure discussed herein addresses dimensional lumber roof systems designed according to the NDS. Where appropriate, the procedure incorporates modifications of the NDS.
When inspecting roof elements or components, the inspector needs to consider the following load combinations (Table 3.1):
- D + (Lr or S)
- 0.6 D + Wu
- D + W
The following sections refer to the span of the member. The NDS defines span as the clear span of the member plus one-half the required bearing at each end of the member. For simplicity, the clear span between bearing points is used herein.
Roofs exhibit system behavior that is, in many respects, similar to floor framing; however, sloped roofs also exhibit unique system behavior. For example, the sheathing membrane or diaphragm on a sloped roof acts as a folded plate that helps resist gravity loads. The effect of the folded plate becomes more pronounced as roof pitch becomes steeper. Such a system effect is usually not considered in design but explains why light wood-framed roof systems may resist loads several times greater than their design capacity. Recent research on trussed roof assemblies with wood structural panel sheathing points to a system capacity increase factor of 1.1 to 1.5 relative to the design of an individual truss. Thus, a conservative system factor of 1.15 is recommended for chord bending stresses, and a factor of 1.1 for chord tension and compression stresses.
Conventional Roof Framing
This section addresses the design of conventional roof rafters, ceiling joists (cross-ties), ridge beams, and hip and valley rafters. The design procedure for a rafter and ceiling joist system is similar to that of a truss, except that the assembly of components and connections is site-built. It is common practice to use a standard pin-joint analysis to determine axial forces in the members and shear forces at their connections. The ceiling joists and rafters are then usually sized according to their individual applied bending loads, taking into account that the axial load effects on the members themselves can be dismissed by judgment based on the large system effects in sheathed roof construction. Frequently, intermediate rafter braces that are similar to truss web members are also used. Standard construction details and span tables for rafters and ceiling joists can be found in The International One- and Two-Family Dwelling Code. These tables generally provide allowable horizontal rafter span with disregard to any difference that roof slope may have on axial and bending loads experienced in the rafters. This approach is generally considered as standard practice.
Structural ridge beams are designed to support roof rafters at the ridge when there are no ceiling joists or cross-ties to resist the outward thrust of rafters that would otherwise occur. A repetitive member factor, Cr, is applicable if the ridge beam is composed of two or more members. It should also be noted that any additional roof system benefit, such as the folded plate action of the roof sheathing diaphragm, goes ignored in its structural contribution to the ridge beam, particularly for steep-sloped roofs.
Roofs with hips and valleys are constructed with rafters framed into a hip or valley rafter as appropriate and, in practice, are typically one to two sizes larger than the rafters they support, e.g., 2x8 or 2x10 hip for 2x6 rafters. While hip and valley rafters experience a unique tributary load pattern or area, they are generally designed much like ridge beams. The folded-plate effect of the roof sheathing diaphragm provides support to a hip or valley rafter in a manner similar to that discussed for ridge beams. However, beneficial system effect generally goes ignored because of the lack of definitive technical guidance. Nonetheless, the use of design judgment should not be ruled out.
Roof Trusses
Roof trusses incorporate rafters (top chords) and ceiling joists (bottom chords) into a structural frame fabricated from 2-inch-thick dimensional lumber, usually 2x4s or 2x6s. A combination of web members are positioned between the top and bottom chords, usually in triangular arrangements that form a rigid framework. Many different truss configurations are possible, including open trusses for attic rooms and cathedral or scissor trusses with sloped top and bottom chords. The wood truss members are connected by metal truss plates punched with barbs (teeth) that are pressed into the truss members. Roof trusses are able to span the entire width of a home without interior support walls, allowing complete freedom in partitioning interior living space.
FIGURE 5.8 Design Methods and Assumptions for a Sloped Roof Rafter

Roof truss manufacturers normally provide the required engineering design based on the loading conditions specified by the building inspector.
The building inspector is responsible for providing the following items to the truss manufacturer for design:
The building inspector should also account for permanent bracing of the truss system at locations designated by the truss inspector. In general, such bracing may involve vertical cross-bracing, runners on the bottom chord, and bracing of certain web members. In typical light-frame residential roof construction, properly attached roof sheathing provides adequate overall bracing of the roof truss system and ceiling finishes normally provide lateral support to the bottom chord of the truss. The only exception is long web members that may experience buckling from excessive compressive loads. Gable end-wall bracing pertains to the role of the roof system in supporting the walls against lateral loads, particularly those produced by wind. Temporary bracing during construction is usually the responsibility of the contractor and is important for worker safety.
The inspector should note that cracking and separation of ceiling finishes may occur at joints between the walls and ceiling of roofs. In the unfavorable condition of high attic humidity, the top chord of a truss may expand while the lower roof members, typically buried under attic insulation, may not be similarly affected. Thus, a truss may bow upward slightly. Other factors that commonly cause interior finish cracking are not in any way associated with the roof truss, including shrinkage of floor framing members, foundation settlement, or heavy loading of a long-span floor resulting in excessive deflection that may pull a partition wall downward from its attachment at the ceiling. To reduce the potential for cracking of ceiling finishes at partition wall intersections, 2x wood blocking should be installed at the top of partition wall plates as a backer for the ceiling finish material (i.e., gypsum board). Ceiling drywall should not be fastened to the blocking or to the truss bottom chord within 16 to 24 inches of the partition. Proprietary clips are available for use in place of wood blocking and resilient metal hat channels may also be used to attach the ceiling finish to the roof framing. Details that show how to minimize partition-ceiling separation problems can be found on the WTCA website at (www.woodtruss.com) or by contacting WTCA to obtain a “Partition Separation” brochure.
Trusses are also frequently used for floor construction to obtain long spans and to allow for the placement of mechanical systems (i.e., ductwork and sanitary drains) in the floor cavity. In addition, trusses have been used to provide a complete house frame (NAHBRC). One efficient use of a roof truss is as a structural truss for the gable end above a garage opening to effectively eliminate the need for a garage door header. For other efficient framing design concepts and ideas, refer to Cost-Effective Home Building: A Design and Construction Handbook (NAHBRC).
Roof Sheathing
Roof sheathing thickness is typically governed by the spacing of roof framing members and live or snow loads. Sheathing is normally in accordance with prescriptive sheathing span rating tables published in a building code or made available by manufacturers. If the limit of the prescriptive tables is exceeded, the inspector may need to perform calculations; however, such calculations are rarely necessary in residential construction.
The fasteners used to attach sheathing to roof rafters are primarily nails. The most popular nail types are sinker, box, and common, of which all have different characteristics that affect structural properties. Proprietary power-driven fasteners (i.e., pneumatic nails and staples) are also used extensively. The building codes and APA tables recommend a fastener schedule for connecting sheathing to roof rafters. Generally, nails are placed at a minimum 6 inches on center at edges and 12 inches on center at intermediate supports. A 6-inch fastener spacing should also be used at the gable-end framing to help brace the gable-end. Nail size is typically 8d, particularly since thinner power driven nails are most commonly used. Roof sheathing is commonly 7/16- to 5/8-inch-thick on residential roofs. Note that in some cases shear loads in the roof diaphragm resulting from lateral loads (i.e., wind and earthquake) may require a more stringent fastening schedule. More importantly, large suction pressures on roof sheathing in high wind areas will require a larger fastener and/or closer spacing. In hurricane-prone regions, it is common to require an 8d deformed shank nail with a 6-inch on-center spacing at all framing connections. At the gable-end truss or rafter, a 4-inch spacing is common.
Roof Overhangs
Overhangs are projections of the roof system beyond the exterior wall line at either the eave or the rake (the sloped gable end). Overhangs protect walls from rain and shade windows from direct sun. When a roof is framed with wood trusses, an eave overhang is typically constructed by extending the top chord beyond the exterior wall. When a roof is framed with rafters, the eave overhang is constructed by using rafters that extend beyond the exterior wall. The rafters are cut with a “bird-mouth” to conform to the bearing support. Gable end overhangs are usually framed by using a ladder panel that cantilevers over the gable end for either stick-framed or truss roofs.
A study completed by the Southern Forest Experiment Station for the U.S. Department of Housing and Urban Development found that the protection afforded by overhangs extends the life of the wall below, particularly if the wall is constructed of wood materials. The report correlates the climate index of a geographic area with a suggested overhang width and recommends highly conservative widths. As a reasonable guideline (given that in many cases no overhang is provided), protective overhang widths should be 12 to 24 inches in damp, humid climates--and more, if practicable. A reasonable rule of thumb to apply is to provide a minimum of 12 inches of overhang width for each story of protected wall below. However, overhang width can significantly increase wind uplift loads on a roof, particularly in high wind regions. The detailing of overhang framing connections (particularly at the rake overhang on a gable end) is a critical consideration in hurricane-prone regions. Often, standard metal clips or straps provide adequate connection. The need for special rake overhang design detailing depends on the length of the overhang, the design wind load condition, and the framing technique that supports the overhang (i.e., 2x outriggers versus cantilevered roof sheathing supporting ladder overhang framing).
Gable-End Wall Bracing
Roof framing provides lateral support to the top of the walls where trusses and rafters are attached to the wall top plate. Likewise, floor framing provides lateral support to the top and bottom of walls, including the top of foundation walls. At a gable end, however, the top of the wall is not directly connected to roof framing members; instead, it is attached to the bottom of a gable-end truss and lateral support at the top of the wall is provided by the ceiling diaphragm. In
higher-wind regions, the joint may become a hinge if the ceiling diaphragm becomes overloaded. Accordingly, it is common practice to brace the top of the end wall (or bottom of the gable end roof framing) with 2x4 or 2x6 framing members that slope upward to the roof diaphragm to attach to a blocking or a ridge beam, as shown in Figure 5.9. Alternatively, braces may be laid flatwise on ceiling joists or truss bottom chords and angled to the walls that are perpendicular to the gable-end wall. Given that braces must transfer inward and outward forces resulting from positive wind pressure or suction on the gable-end wall, they are commonly attached to the top of the gable-end wall with straps to transfer tension forces that may develop in hurricanes and other extreme wind conditions. The need for and special detailing of gable-end wall braces depends on the height and area of the gable end (i.e., tributary area) and the design wind load. The gable end-wall can also be braced by the use of a wood structural panel attached to the gable end framing and the ceiling framing members.
As an alternative to the above strategy, the gable-end wall may be framed with continuous studs that extend to the roof sheathing at the gable end (i.e., balloon-framed). If the gable end-wall encloses a two-story room, such as a room with a cathedral ceiling, it is especially important that the studs extend to the roof sheathing; otherwise, a hinge may develop in the wall and cause cracking of wall finishes (even in a moderate wind) and could easily precipitate failure of the wall in an extreme wind. Depending on wall height, stud size, stud spacing, and the design wind load condition, taller, full-height studs may need to be increased in size to meet deflection or bending capacity requirements. Some inspector judgment should be exercised in this framing application with respect to the application of deflection criteria.
FIGURE 5.9 Typical Roof Overhang Construction

Table 5.6 may assist in dealing with the need to meet a reasonable serviceability limit for deflection.
Finally, as an alternative that avoids the gable end-wall bracing problem, a hip roof may be used. The hip shape is inherently more resistant to wind damage in hurricane-prone wind environments and braces the end walls against lateral wind loads by direct attachment to rafters.
- design loads;
- truss profile;
- support locations; and
- any special requirements.
The building inspector should also account for permanent bracing of the truss system at locations designated by the truss inspector. In general, such bracing may involve vertical cross-bracing, runners on the bottom chord, and bracing of certain web members. In typical light-frame residential roof construction, properly attached roof sheathing provides adequate overall bracing of the roof truss system and ceiling finishes normally provide lateral support to the bottom chord of the truss. The only exception is long web members that may experience buckling from excessive compressive loads. Gable end-wall bracing pertains to the role of the roof system in supporting the walls against lateral loads, particularly those produced by wind. Temporary bracing during construction is usually the responsibility of the contractor and is important for worker safety.
The inspector should note that cracking and separation of ceiling finishes may occur at joints between the walls and ceiling of roofs. In the unfavorable condition of high attic humidity, the top chord of a truss may expand while the lower roof members, typically buried under attic insulation, may not be similarly affected. Thus, a truss may bow upward slightly. Other factors that commonly cause interior finish cracking are not in any way associated with the roof truss, including shrinkage of floor framing members, foundation settlement, or heavy loading of a long-span floor resulting in excessive deflection that may pull a partition wall downward from its attachment at the ceiling. To reduce the potential for cracking of ceiling finishes at partition wall intersections, 2x wood blocking should be installed at the top of partition wall plates as a backer for the ceiling finish material (i.e., gypsum board). Ceiling drywall should not be fastened to the blocking or to the truss bottom chord within 16 to 24 inches of the partition. Proprietary clips are available for use in place of wood blocking and resilient metal hat channels may also be used to attach the ceiling finish to the roof framing. Details that show how to minimize partition-ceiling separation problems can be found on the WTCA website at (www.woodtruss.com) or by contacting WTCA to obtain a “Partition Separation” brochure.
Trusses are also frequently used for floor construction to obtain long spans and to allow for the placement of mechanical systems (i.e., ductwork and sanitary drains) in the floor cavity. In addition, trusses have been used to provide a complete house frame (NAHBRC). One efficient use of a roof truss is as a structural truss for the gable end above a garage opening to effectively eliminate the need for a garage door header. For other efficient framing design concepts and ideas, refer to Cost-Effective Home Building: A Design and Construction Handbook (NAHBRC).
Roof Sheathing
Roof sheathing thickness is typically governed by the spacing of roof framing members and live or snow loads. Sheathing is normally in accordance with prescriptive sheathing span rating tables published in a building code or made available by manufacturers. If the limit of the prescriptive tables is exceeded, the inspector may need to perform calculations; however, such calculations are rarely necessary in residential construction.
The fasteners used to attach sheathing to roof rafters are primarily nails. The most popular nail types are sinker, box, and common, of which all have different characteristics that affect structural properties. Proprietary power-driven fasteners (i.e., pneumatic nails and staples) are also used extensively. The building codes and APA tables recommend a fastener schedule for connecting sheathing to roof rafters. Generally, nails are placed at a minimum 6 inches on center at edges and 12 inches on center at intermediate supports. A 6-inch fastener spacing should also be used at the gable-end framing to help brace the gable-end. Nail size is typically 8d, particularly since thinner power driven nails are most commonly used. Roof sheathing is commonly 7/16- to 5/8-inch-thick on residential roofs. Note that in some cases shear loads in the roof diaphragm resulting from lateral loads (i.e., wind and earthquake) may require a more stringent fastening schedule. More importantly, large suction pressures on roof sheathing in high wind areas will require a larger fastener and/or closer spacing. In hurricane-prone regions, it is common to require an 8d deformed shank nail with a 6-inch on-center spacing at all framing connections. At the gable-end truss or rafter, a 4-inch spacing is common.
Roof Overhangs
Overhangs are projections of the roof system beyond the exterior wall line at either the eave or the rake (the sloped gable end). Overhangs protect walls from rain and shade windows from direct sun. When a roof is framed with wood trusses, an eave overhang is typically constructed by extending the top chord beyond the exterior wall. When a roof is framed with rafters, the eave overhang is constructed by using rafters that extend beyond the exterior wall. The rafters are cut with a “bird-mouth” to conform to the bearing support. Gable end overhangs are usually framed by using a ladder panel that cantilevers over the gable end for either stick-framed or truss roofs.
A study completed by the Southern Forest Experiment Station for the U.S. Department of Housing and Urban Development found that the protection afforded by overhangs extends the life of the wall below, particularly if the wall is constructed of wood materials. The report correlates the climate index of a geographic area with a suggested overhang width and recommends highly conservative widths. As a reasonable guideline (given that in many cases no overhang is provided), protective overhang widths should be 12 to 24 inches in damp, humid climates--and more, if practicable. A reasonable rule of thumb to apply is to provide a minimum of 12 inches of overhang width for each story of protected wall below. However, overhang width can significantly increase wind uplift loads on a roof, particularly in high wind regions. The detailing of overhang framing connections (particularly at the rake overhang on a gable end) is a critical consideration in hurricane-prone regions. Often, standard metal clips or straps provide adequate connection. The need for special rake overhang design detailing depends on the length of the overhang, the design wind load condition, and the framing technique that supports the overhang (i.e., 2x outriggers versus cantilevered roof sheathing supporting ladder overhang framing).
Gable-End Wall Bracing
Roof framing provides lateral support to the top of the walls where trusses and rafters are attached to the wall top plate. Likewise, floor framing provides lateral support to the top and bottom of walls, including the top of foundation walls. At a gable end, however, the top of the wall is not directly connected to roof framing members; instead, it is attached to the bottom of a gable-end truss and lateral support at the top of the wall is provided by the ceiling diaphragm. In
higher-wind regions, the joint may become a hinge if the ceiling diaphragm becomes overloaded. Accordingly, it is common practice to brace the top of the end wall (or bottom of the gable end roof framing) with 2x4 or 2x6 framing members that slope upward to the roof diaphragm to attach to a blocking or a ridge beam, as shown in Figure 5.9. Alternatively, braces may be laid flatwise on ceiling joists or truss bottom chords and angled to the walls that are perpendicular to the gable-end wall. Given that braces must transfer inward and outward forces resulting from positive wind pressure or suction on the gable-end wall, they are commonly attached to the top of the gable-end wall with straps to transfer tension forces that may develop in hurricanes and other extreme wind conditions. The need for and special detailing of gable-end wall braces depends on the height and area of the gable end (i.e., tributary area) and the design wind load. The gable end-wall can also be braced by the use of a wood structural panel attached to the gable end framing and the ceiling framing members.
As an alternative to the above strategy, the gable-end wall may be framed with continuous studs that extend to the roof sheathing at the gable end (i.e., balloon-framed). If the gable end-wall encloses a two-story room, such as a room with a cathedral ceiling, it is especially important that the studs extend to the roof sheathing; otherwise, a hinge may develop in the wall and cause cracking of wall finishes (even in a moderate wind) and could easily precipitate failure of the wall in an extreme wind. Depending on wall height, stud size, stud spacing, and the design wind load condition, taller, full-height studs may need to be increased in size to meet deflection or bending capacity requirements. Some inspector judgment should be exercised in this framing application with respect to the application of deflection criteria.
FIGURE 5.9 Typical Roof Overhang Construction

Table 5.6 may assist in dealing with the need to meet a reasonable serviceability limit for deflection.
Finally, as an alternative that avoids the gable end-wall bracing problem, a hip roof may be used. The hip shape is inherently more resistant to wind damage in hurricane-prone wind environments and braces the end walls against lateral wind loads by direct attachment to rafters.
Structural Design Concepts for the Home Inspector
Structural Design Loads for the Home Inspector
Structural Design of Foundations for the Home Inspector
Structural Design Loads for the Home Inspector
Structural Design of Foundations for the Home Inspector

